Быстрая навигация по странице:
Понятие дисперсии кратко
Дисперсия – это критерий, позволяющий оценить меру рассеяния конкретных величин исследуемого признака относительно их средней величины (или математического ожидания). В статистике дисперсия является одним из абсолютных показателей вариации. Дисперсия является средним квадратом отклонений индивидуальных величин исследуемого признака от генеральной средней и обозначается как σ2 (читается как «сигма квадрат»). На применении дисперсии базируется множество методов математической статистики. Существенное прикладное значение имеет правило сложения дисперсий.
Размещено на www.rnz.ru
Вернуться назад: помощь в решении задач по статистике
Интерпретация значения дисперсии следующая: например, если исследуется вариация какого-то признака, и получено значение дисперсии 13.45 млн. руб., то можно сделать следующий вывод: полученное значение дисперсии говорит о том, что средний квадрат отклонений признака относительно его среднего значения составил 13.45 млн. руб.
⇑Наверх⇑
Формулы расчета дисперсии
Для расчета обычной дисперсии применяется следующая формула:
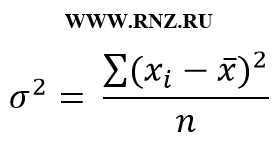
Такая формула генеральной дисперсии в выборке дает смещенную оценку. Поэтому в случае, если требуется определить величину несмещенной дисперсии, то используют следующую формулу:
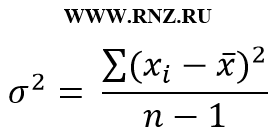
Для расчета взвешенной дисперсии применяют следующую формулу:
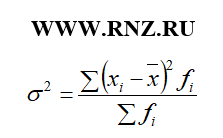
В том случае, если для определения величины дисперсии используется способ отсчета от условного нуля, то дисперсия по рассчитывается по следующей формуле:
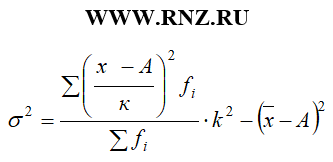
где k – ширина интервала
А – условный нуль, в качестве которого используют середину интервала с наибольшей частотой.
В том случае, если вычисление дисперсии осуществляется по способу моментов, то применяется следующая формула:
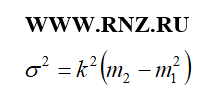
где m1 - начальный момент первого порядка;
где m2 - начальный момент второго порядка.
Дисперсия может быть вычислена и с использованием средних величин:
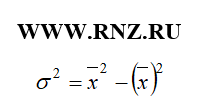
где первое число - среднее значение из квадратов значений признака;
второе число (вычитаемое) - квадрат среднего значения признака.
Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
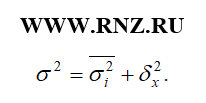
Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида (закон сложения дисперсий).
Средняя из внутригрупповых дисперсий определяется по формуле:
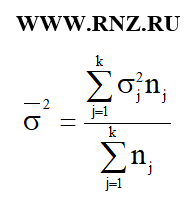
Межгрупповая дисперсия вычисляется по формуле:
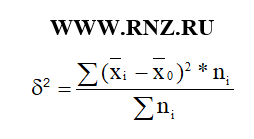
⇑Наверх⇑
Пример расчета дисперсии
Даны следующие значения банковских вкладов в тыс. руб.: 17,1; 28,2; 18,5; 25,1; 13,7; 28; 12,8; 17; 15,3; 13,9.
Определить значение выборочной дисперсии и несмещенную оценку дисперсии.
Решение:
Составим расчетную таблицу
| № п/п | Xi | (Xi - Xсреднее)2 |
|---|---|---|
| 1 | 17,1 | 3,46 |
| 2 | 28,2 | 85,378 |
| 3 | 18,5 | 0,212 |
| 4 | 25,1 | 37,7 |
| 5 | 13,7 | 27,668 |
| 6 | 28 | 81,722 |
| 7 | 12,8 | 37,946 |
| 8 | 17 | 3,842 |
| 9 | 15,3 | 13,396 |
| 10 | 13,9 | 25,604 |
| Итого | 189,6 | 316,928 |
| Среднее | 18,96 | -- |
Расчет выполним по приведенным выше формулам:
Дисперсия σ2 = 316,928 / 10 = 31,69 тыс. руб.
Несмещенная дисперсия: σ2 = 316,928 / (10-1) = 35,21 тыс. руб.
⇑Наверх⇑
Онлайн-калькулятор расчета дисперсии
Представляем небольшой онлайн – калькулятор, используя который Вы можете вычислить значения простой и несмещенной дисперсии. При заполнении приведенной формы калькулятора внимательно соблюдайте размерность полей, что позволит быстро и точно выполнить вычисления. В приведенной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает и посмотреть, как правильно заполнять поля. Для определения значений соответствующих показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку "Выполнить вычисления". При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точкой, а не запятой!
Максимальное количество значений, для которых может быть рассчитана дисперсия онлайн – составляет 20. Вы их можете добавить, нажимая кнопку "Добавить строку".
Онлайн-калькулятор дисперсии
⇑Наверх⇑

