Решенные задачи по методам оптимальных решений, контрольная

Решенные задачи по методам оптимальных решений, контрольная

ЭММ
Решенные задачи по методам оптимальных решений

 

Решенные задачи по методам оптимальных решений, контрольная

План (содержание) работы Решенные задачи по методам оптимальных решений:

Решенная задача по методам оптимальных решений №1

Таблица (задания 1-20) содержит данные баланса трех отраслей промышленности за отчетный период. Требуется:

1) Убедиться, что модель продуктивна, т.е. найти матрицу коэффициентов прямых затрат и убедиться в том, что она продуктивна;

2) Составить баланс производства и распределения продукции;

3) Найти конечный продукт (вектор конечного продукта yсреднее) каждой отрасли для новых значений валовых продуктов отраслей (нового вектора валового выпуска): значения нового вектора валового выпуска больше соответствующих значений старого вектора валового выпуска на 10 единиц; так, например, в задаче 1 старые значения вектора валового выпуска x1 = 120, x2 = 140, x3 = 140, а новые значения вектора валового выпуска x1 = 160, x2 = 150, x3 = 150;

4) Найти валовой продукт (вектор валового выпуска xсреднее) каждой отрасли для новых значений конечных продуктов отраслей (нового вектора конечного продукта): значения нового вектора конечного продукта больше соответствующих значений старого вектора конечного продукта на 10 единиц; так, например, в задаче 1 старые значения вектора конечного продукта y1 = 40, y2 = 25, y3 = 35, а новые значения вектора конечного продукта y1 = 50, y2 = 35, y3 = 45;

Данные баланса трех отраслей промышленности за отчетный период:

№ п.п.
Производящие отрасли
Потребляющие отрасли
Конечный продукт
Валовой продукт
1
2
3
1
Машиностроение
30
20
40
40
130
2
Ракетостроение
25
50
60
35
170
3
Нефтехимия
30
40
35
35
140
Условно чистая продукция
45
60
5
110
Валовой продукт
130
170
140
440

 

Решенная задача по методам оптимальных решений №2

Для рис. 2 и заданного варианта определить характеристики СПУ:

1) ранние и поздние сроки совершения событий;

2) резервы времени событий;

3) критический путь и его длину, пояснить смысл найденной величины (длина критического пути);

4) для некритических работ найти полные, свободные и независимые резервы времени;

5) для некритических работ найти коэффициенты напряженности и пояснить за счет каких работ возможна оптимизация сетевой модели.

Рис.2.:

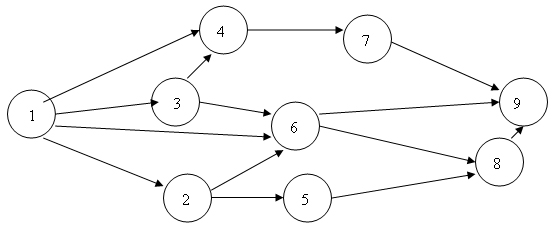
оптимизация сетевой модели
оптимизация сетевой модели

 

полные, свободные и независимые резервы времени:

Т(1, 2)
Т(1, 3)
Т(1, 4)
Т(1, 6)
Т(2, 5)
Т(2, 6)
Т(3, 4)
10
19
5
11
12
16
14
Т(3, 6)
Т(4, 7)
Т(5, 8)
Т(6, 8)
Т(6, 9)
Т(7, 9)
Т(8, 9)
11
18
6
10
11
15
14

 

Цена консультации по работе Решенные задачи по методам оптимальных решений - договорная.

Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку: