Линейное уравнение множественной регрессии
План (содержание) работы Линейное уравнение множественной регрессии:
Понятие уравнения множественной регрессии
Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. Построение линейного уравнения множественной регрессии в общем случае включает следующие этапы: обоснование линейной формы для создаваемой модели; отбор факторных признаков; обеспечение достаточного объема совокупности для получения несмещенных оценок.
Вы можете купить решение задач на множественную регрессию
При моделировании экономических процессов при помощи многофакторных функций наибольшее распространение получило линейное уравнение множественной регрессии. Частое применение такого уравнения многофакторной зависимости объясняется сравнительной простотой как его построения, так и интерпретации параметров. Необходимо отметить, что коэффициенты получаемой модели в общем случае несопоставимы друг с другом из-за разных единиц измерения исходных параметров. В том случае, когда в линейную модель многофакторной зависимости в качестве переменных входят взаимозаменяемые производственные ресурсы, тогда получаемая модель позволяет определить норму замещения одного фактора производства другим.
Смотрите так же: Помощь по эконометрике
Размещено на www.rnz.ru
Обоснование линейной формы уравнения множественной регрессии затрудняется тем, что для любой формы зависимости можно выбрать целый ряд функций, которые в определенной мере будут описывать эти связи. Поскольку линейная модель многофакторной зависимости результирующего признака от различных переменных строится главным образом для объяснения и количественного выражения взаимосвязей, она должна хорошо отражать сложившиеся между исследуемыми факторами фактические связи. Наиболее приемлемым способом отбора факторных признаков при построении линейной модели многофакторной зависимости является шаговая регрессия (шаговый регрессионный анализ). Сущность указанного метода заключается в последовательном включении (исключении) переменных в создаваемую регрессионную модель и дальнейшей проверке их значимости. Переменные поочередно включаются в модель посредством так называемого прямого метода. В процессе исследования значимости добавленной переменной вычисляется, насколько снижается сумма квадратов остатков и повышается значение множественного коэффициента корреляции.
Формула линейного уравнения множественной регрессии
При исследовании зависимости результативного признака от двух и более факторных признаков, может потребовать построение, как правило, следующих видов уравнений множественной регрессии:
- линейное уравнение множественной регрессии:
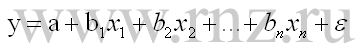
- степенная множественная регрессия:
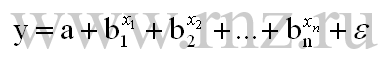
- экспоненциальное уравнение множественной регрессии:
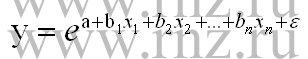
- гиперболическое уравнение многофакторной зависимости:
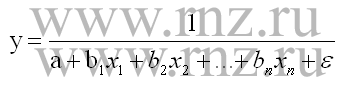
Пример построения уравнения множественной регрессии матричным методом
Приведем пример построения множественной регрессионной модели матричным способом и при помощи MS Excel. Условные исходные данные следующие: имеются показатели товарооборота торгового предприятия Y (тыс. руб.), а также количество сотрудников Х1 (чел) и затрат на рекламу Х2 (тыс. руб.).
| № п/п | Y | Х1 | Х2 |
|---|---|---|---|
| 1 | 473,8 | 34 | 155,8 |
| 2 | 480,7 | 45 | 176,1 |
| 3 | 486,4 | 42 | 189 |
| 4 | 532,7 | 61 | 197 |
| 5 | 547,9 | 58 | 182 |
По указанным исходным данным необходимо построить модель, показывающую зависимость товарооборота от количества сотрудников и расходов на рекламу.
На первом шаге напишем основные матрицы, на базе которых и будут производиться дальнейшие вычисления.
Задание 2
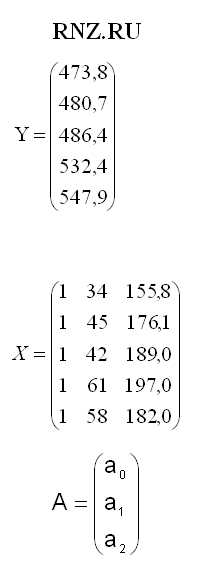
Уравнение множественной регрессии в матричной форме имеет вид: Y = XA.
Составим транспонированную матрицу:
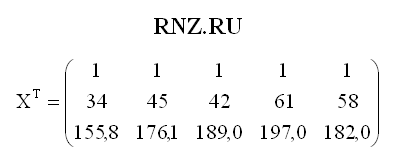
В Excel это можно сделать при помощи встроенной функции ТРАНСП(). Данная функция применяется для смены направления отображения содержимого ячеек рабочего листа Excel с горизонтального расположения на вертикальное и наоборот. При использовании указанной функции сами исходные данные не меняются.
Далее вычисляем произведение матриц ХТ*Х:

В Excel такое произведение матриц можно вычислить при помощи встроенной функции МУМНОЖ(). При задании этой функции необходимо обозначить ссылки на одну из тех матриц, произведение которых необходимо получить. Важным требованием для использования МУМНОЖ() выступает то, что число строк одной матрицы должно соответствовать числу столбцов другой. Если это условие не соблюдается, то при выполнении операции умножения будет выдана ошибка. Для корректной работы функции необходимо следить и за тем, чтобы отсутствовали пустые элементы перемножаемых матриц, и, естественно, они должны состоять из чисел.
Рассчитываем произведение матриц ХТ*Y:
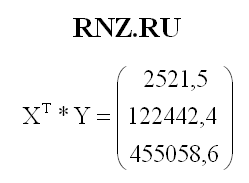
В Excel для этого также можно использовать уже указанную функцию МУМНОЖ().
Вычислим обратную матрицу (ХТ*Х)-1:

В Excel для нахождения обратной матрицы можно использовать встроенную функцию МОБР(). При использовании данной функции необходимо соблюдать условие о том, что количество строк должно быть равно количеству столбов, не должно содержаться пустых элементов или текстовых значений.
В заключении рассчитаем матрицу коэффициентов модели многофакторной зависимости:
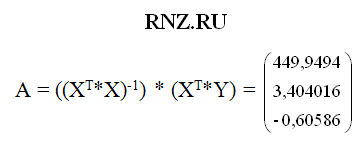
Таким образом, получим следующее уравнение множественной регрессии в естественной форме: Y^ = 449,95+3,404*х1-0,6059*х2. Далее можно посмотреть экономическую интерпретацию коэффициентов линейной модели многофакторной зависимости. Правильная интерпретация коэффициентов построенной модели важна для оценки силы влияния независимой переменной на результирующую. Выполнение такого сравнения силы влияния разных переменных возможно при построении уравнения в стандартизированном масштабе, которое можно построить на базе матрицы парных коэффициентов корреляции.
Вы можете заказать построение множественной регрессии по Вашим исходным данным
Приводим примеры условий решенных задач на построение линейного уравнения множественной регрессии:
Задача №1
По 20 предприятиям региона (см. таблицу) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).
| Номер предприятия | y | x1 | x2 | Номер предприятия | y | x1 | x2 |
|---|---|---|---|---|---|---|---|
| 1 | 7 | 3,9 | 10 | 11 | 9 | 6 | 21 |
| 2 | 7 | 3,9 | 14 | 12 | 11 | 6,4 | 22 |
| 3 | 7 | 3,7 | 15 | 13 | 9 | 6,8 | 22 |
| 4 | 7 | 4 | 16 | 14 | 11 | 7,2 | 25 |
| 5 | 7 | 3,8 | 17 | 15 | 12 | 8 | 28 |
| 6 | 7 | 4,8 | 19 | 16 | 12 | 8,2 | 29 |
| 7 | 8 | 5,4 | 19 | 17 | 12 | 8,1 | 30 |
| 8 | 8 | 4,4 | 20 | 18 | 12 | 8,5 | 31 |
| 9 | 8 | 5,3 | 20 | 19 | 14 | 9,6 | 32 |
| 10 | 10 | 6,8 | 20 | 20 | 14 | 9 | 36 |
Требуется:
1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.
2. Проанализировать линейные коэффициенты парной и частной корреляции.
3. Написать уравнение множественной регрессии, оценить значимость его параметров, пояснить их экономический смысл.
4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и R2yx1x2. Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.
5. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х1 после x2 и фактора х2 после х1.
6. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача №2
В табл. представлены результаты наблюдений за x1, x2 и y:
| x1 | 3001 | 3101 | 3543 | 3237 | 3330 | 3808 | 2415 | 3295 | 3504 | 3056 | 3007 | 2844 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x2 | 78.2 | 68 | 77.2 | 77.2 | 77.2 | 75.7 | 62.6 | 78 | 78.2 | 79 | 67.6 | 69.8 |
| y | 0.922 | 0.763 | 0.923 | 0.918 | 0.906 | 0.905 | 0.545 | 0.894 | 0.9 | 0.932 | 0.74 | 0.701 |
1) Найти МНК-оценки параметров уравнения множественной линейной регрессии вида y = β0 + β1x1+ β2x2 + ε. Пояснить смысл полученных результатов.
2) Проверить значимость оценок параметров уравнения регрессии при уровне значимости 0,05. Сделать выводы.
3) Найти доверительные интервалы для параметров уравнения регрессии при доверительной вероятности 0,95. Пояснить смысл полученных результатов.
4) Найти коэффициент детерминации. Сделать вывод.
5) Проверить значимость уравнения регрессии (коэффициента детерминации) при уровне значимости 0,05. Сделать вывод.
6) Проверить наличие гомоскедастичности при уровне значимости 0,05 (с помощью теста ранговой корреляции Спирмена). Сделать вывод.
7) Проверить наличие автокорреляции при уровне значимости 0,05 (с помощью теста Дарбина-Уотсона). Сделать вывод.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача №3
По данным за два года изучается зависимость оборота розничной торговли (Y, млрд. руб.) от ряда факторов: X1 - денежные доходы населения, млрд. руб.; Х2 – доля доходов, используемая на покупку товаров и оплату услуг, млрд. руб.; Х3 – численность безработных, млн. чел.; Х4 – официальный курс рубля по отношению к доллару США.
Таблица 12
| Месяц | Y | X1 | X2 | X3 | X4 |
|---|---|---|---|---|---|
| 1 | 72,9 | 117,7 | 81,6 | 8,3 | 6,026 |
| 2 | 67 | 123,8 | 73,2 | 8,4 | 6,072 |
| 3 | 69,7 | 126,9 | 75,3 | 8,5 | 6,106 |
| 4 | 70 | 134,1 | 71,3 | 8,5 | 6,133 |
| 5 | 69,8 | 123,1 | 77,3 | 8,3 | 6,164 |
| 6 | 69,1 | 126,7 | 76 | 8,1 | 6,198 |
| 7 | 70,7 | 130,4 | 76,6 | 8,1 | 6,238 |
| 8 | 80,1 | 129,3 | 84,7 | 8,3 | 7,905 |
| 9 | 105,2 | 145,4 | 92,4 | 8,6 | 16,065 |
| 10 | 102,5 | 163,8 | 80,3 | 8,9 | 16,01 |
| 11 | 108,7 | 164,8 | 82,6 | 9,4 | 17,88 |
| 12 | 134,8 | 227,2 | 70,9 | 9,7 | 20,65 |
| 13 | 116,7 | 164 | 89,9 | 10,1 | 22,6 |
| 14 | 117,8 | 183,7 | 81,3 | 10,4 | 22,86 |
| 15 | 128,7 | 195,8 | 83,7 | 10 | 24,18 |
| 16 | 129,8 | 219,4 | 76,1 | 9,6 | 24,23 |
| 17 | 133,1 | 209,8 | 80,4 | 9,1 | 24,44 |
| 18 | 136,3 | 223,3 | 78,1 | 8,8 | 24,22 |
| 19 | 139,7 | 223,6 | 79,8 | 8,7 | 24,19 |
| 20 | 151 | 236,6 | 82,1 | 8,6 | 24,75 |
| 21 | 154,6 | 236,6 | 83,2 | 8,7 | 25,08 |
| 22 | 160,2 | 248,6 | 80,8 | 8,9 | 26,05 |
| 23 | 163,2 | 253,4 | 81,8 | 9,1 | 26,42 |
| 24 | 191,7 | 351,4 | 68,3 | 9,1 | 27 |
Задание:
1. Для заданного набора данных постройте линейную модель множественной регрессии. Оцените точность и адекватность построенного уравнения регрессии.
2. Выделите значимые и незначимые факторы в модели. Постройте уравнение регрессии со статистически значимыми факторами. Дайте экономическую интерпретацию параметров модели.
3. Рассчитайте стандартизованные коэффициенты модели и запишите уравнение регрессии в стандартизованном виде. Упорядочите факторы по степени влияния на оборот розничной торговли?
4. Для полученной модели проверьте выполнение условия гомоскедастичности остатков, применив тест Голдфельда-Квандта.
5. Проверьте полученную модель на наличие автокорреляции остатков с помощью теста Дарбина-Уотсона.
6. Проверьте, адекватно ли предположение об однородности исходных данных в регрессионном смысле. Можно ли объединить две выборки (по первым 12 и остальным наблюдениям) в одну и рассматривать единую модель регрессии Y по X?
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача №4 на построение множественной регрессии
Исследователи, проанализировав деятельность 10 фирм, получили следующие данные зависимости объема выпуска продукции (y) от количества рабочих (х1) и стоимости основных фондов (тыс.руб.) (х2)
| y | x1 | x2 | y2 | x21 | x22 | yx1 | yx2 | x1x2 | |
|---|---|---|---|---|---|---|---|---|---|
| ∑ | 666.9 | 373.4 | 566 | 44512.81 | 13953,58 | 32060 | 24919,9 | 37757,5 | 21143,8 |
Требуется:
1. Определить парные коэффициенты корреляции. Сделать вывод.
2. Построить уравнение множественной регрессии в стандартизированном масштабе и естественной форме. Сделать экономический вывод.
3. Определить множественный коэффициент корреляции. Сделать вывод.
4. Найти множественный коэффициент детерминации. Сделать вывод.
5. Определить статистическую значимость уравнения с помощью F-критерия. Сделать вывод.
6. Найти прогнозное значение объема продукции, при условии, что количество рабочих составит 10 человек, а стоимость основных фондов 30 тыс.руб. Ошибка прогноза равна 3,78. Провести точечный и интервальный прогноз. Сделать вывод.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача №5
В табл. представлены результаты наблюдений за x1, x2 и y:
| x1 | 3001 | 3101 | 3543 | 3237 | 3330 | 3808 | 2415 | 3295 | 3504 | 3056 | 3007 | 2844 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x2 | 78.2 | 68 | 77.2 | 77.2 | 77.2 | 75.7 | 62.6 | 78 | 78.2 | 79 | 67.6 | 69.8 |
| y | 0.922 | 0.763 | 0.923 | 0.918 | 0.906 | 0.905 | 0.545 | 0.894 | 0.9 | 0.932 | 0.74 | 0.701 |
1) Найти МНК-оценки параметров уравнения множественной линейной регрессии вида y = β0 + β1x1+ β2x2 + ε. Пояснить смысл полученных результатов.
2) Проверить значимость оценок параметров уравнения регрессии при уровне значимости 0,05. Сделать выводы.
3) Найти доверительные интервалы для параметров уравнения регрессии при доверительной вероятности 0,95. Пояснить смысл полученных результатов.
4) Найти коэффициент детерминации. Сделать вывод.
5) Проверить значимость уравнения регрессии (коэффициента детерминации) при уровне значимости 0,05. Сделать вывод.
6) Проверить наличие гомоскедастичности при уровне значимости 0,05 (с помощью теста ранговой корреляции Спирмена). Сделать вывод.
7) Проверить наличие автокорреляции при уровне значимости 0,05 (с помощью теста Дарбина-Уотсона). Сделать вывод.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача №6
По 30 регионам страны известны данные о валовом региональном продукте (y, млн. руб.), балансовой стоимости оборудования (х1, млн. руб.), числе занятых (х2, тыс. чел).
Предварительная обработка данных имеет следующие результаты: ∑y = 158015,9; ∑x1 = 397939; ∑x2 = 22051,1; ∑yx1 = 2360874891; ∑ух2 = 130570309,7; ∑x1х2 = 328735350,8; ∑y2 = 939878516,6; ∑x21 = 6035509137; ∑x22 = 19954309,73; ∑|y-Y^|/y = 3,268
Задание:
1. Построить двухфакторное линейное уравнение регрессии.
2. Определить парные и частные коэффициенты корреляции, сделать соответствующие выводы.
3. Рассчитать коэффициенты множественной корреляции, детерминации (в том числе скорректированный). Проанализировать результаты.
4. Оценить значимость полученного уравнения с помощью F-критерия Фишера и качество модели с помощью ошибки аппроксимации.
5. Определить частные коэффициенты эластичности и сделайте выводы.
Эта задача уже решена! Вы можете получить её за 150 руб.
Цена консультации по работе Линейное уравнение множественной регрессии - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:
