Решенные задачи по теории статистики из практикума Р.А. Шмойловой, контрольная
План (содержание) работы Решенные задачи по теории статистики из практикума Р.А. Шмойловой:
Контрольная работа №1
I Блок
Задача 3.8
Имеются следующие данные об успеваемости 30 студентов группы по теории статистики в летнюю сессию 2003 г.: 5, 4, 3, 3, 5, 4, 4, 4, 3, 4, 4, 5, 4, 4, 3, 2, 5, 3, 4, 4, 4, 3, 2, 5, 2, 5, 5, 2, 3, 3.
Постройте:
а) ряд распределения студентов по оценкам, полученным в сессию, и изобразите его графически;
б) ряд распределения студентов по уровню успеваемости, выделив в нем две группы студентов: неуспевающих (2балла), успевающих (3 балла и выше);
в) укажите, каким видом ряда распределения (вариационным или атрибутивным) является каждый из этих двух рядов.
Эта задача уже решена! Получите файл за 150 руб.
Смотрите так же примеры решений задач по статистике
Задача 3.10
Известны следующие данные по основным показателям деятельности крупнейших банков одной из областей Российской Федерации (данные условные), (млн.руб.):
| № п/п | Сумма активов | Собственный капитал | Привлеченные ресурсы | Балансовая прибыль | Объем вложений в государственные ценные бумаги | Ссудная задолженность |
|---|---|---|---|---|---|---|
| 1 | 645,6 | 12 | 27,1 | 8,1 | 3,5 | 30,8 |
| 2 | 636,9 | 70,4 | 56,3 | 9,5 | 12,6 | 25,7 |
| 3 | 629 | 41 | 95,7 | 38,4 | 13,3 | 26,4 |
| 4 | 619,6 | 120,8 | 44,8 | 38,4 | 4,4 | 25,3 |
| 5 | 616,4 | 49,4 | 108,7 | 13,4 | 15 | 20,9 |
| 6 | 614,4 | 50,3 | 108,1 | 30,1 | 19,1 | 47,3 |
| 7 | 608,6 | 70 | 76,1 | 37,8 | 19,2 | 43,7 |
| 8 | 601,1 | 52,4 | 26,3 | 41,1 | 3,7 | 29,1 |
| 9 | 600,2 | 42 | 46 | 9,3 | 5,2 | 56,1 |
| 10 | 600 | 27,3 | 24,4 | 39,3 | 13,1 | 24,9 |
| 11 | 592,9 | 72 | 65,5 | 8,6 | 16,7 | 39,6 |
| 12 | 591,7 | 22,4 | 76 | 40,5 | 7,5 | 59,6 |
| 13 | 585,5 | 39,3 | 106,9 | 45,3 | 6,7 | 44,9 |
| 14 | 578,6 | 70 | 89,5 | 8,4 | 11,2 | 32,2 |
| 15 | 577,5 | 22,9 | 84 | 12,8 | 19,3 | 45,1 |
| 16 | 553,7 | 119,3 | 89,4 | 44,7 | 19,4 | 24,5 |
| 17 | 543,6 | 49,6 | 93,8 | 8,8 | 5,7 | 31,1 |
| 18 | 542 | 88,6 | 26,7 | 32,2 | 7,8 | 37,1 |
| 19 | 517 | 43,7 | 108,1 | 20,3 | 8,3 | 23,1 |
| 20 | 516,7 | 90,5 | 25,2 | 12,2 | 9,7 | 15,8 |
1. Постройте группировку коммерческих банков по величине собственного капитала, выделив четыре группы с равными интервалами. Рассчитайте по каждой группе сумму активов, собственный капитал, привлеченные ресурсы, балансовую прибыль. Результаты группировки представьте в табличной форме и сформулируйте выводы.
2. Постройте полигон и гистограмму распределения банков по величине собственного капитала.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 3.18
Имеются следующие данные о распределении промышленных предприятий двух регионов по численности занятого на них промышленно - производственного персонала (ППП):
| Регион 1 | Регион 2 | ||||
|---|---|---|---|---|---|
| Группы предприятий по численности работающих, чел. | Число предприятий, % | Численность промышленно-производственного персонала, тыс.чел. | Группы предприятий по численности работающих, чел. | Число предприятий, % | Численность промышленно-производственного персонала, тыс.чел. |
| До 100 | 32 | 1 | До 300 | 34 | 1 |
| 101-500 | 38 | 4 | 301-600 | 28 | 6 |
| 501-1000 | 17 | 10 | 601-1000 | 20 | 10 |
| 1001-2000 | 9 | 15 | 1001-2000 | 13 | 15 |
| 2001-5000 | 3 | 32 | 2001-4000 | 4 | 43 |
| 5001 и более | 1 | 38 | 4001 и более | 1 | 25 |
| Итого | 100 | 100 | Итого | 100 | 100 |
Постройте вторичную группировку данных о распределении промышленных предприятий, пересчитав данные:
а) региона 2 в соответствии с группировкой региона 1;
б) региона 1 в соответствии с группировкой региона 2;
в) регионов 1 и 2, образовав следующие группы промышленных предприятий по численности ППП: до 500, 500 - 1000,1000 - 2000, 2000 - 3000, 3000 - 4000,4000 - 5000,5000 и более.
Эта задача уже решена! Получите файл за 150 руб.
II Блок
Задача 6.2
Имеются следующие данные о производстве бумаги в РФ:
| 1998 | 1999 | 2000 | 2001 | |
|---|---|---|---|---|
| Произведено бумаги, тыс.т. | 2453 | 2968 | 3326 | 3415 |
Вычислите относительные показатели динамики с переменной и постоянной базой сравнения. Проверьте их взаимосвязь.
Решение задачи:
Относительные показатели динамики с переменной базой сравнения определим по формуле: ОПД = Текущий показатель / Предшествующий показатель
Переменная база сравнения (цепные показатели):
ОПД1 = 2968 / 2453*100% = 120.99%;
ОПД2 = 3326 / 2968 * 100% = 112.06%;
ОПД3 = 3415 / 3326 * 100% = 102.68%.
Относительные показатели динамики с постоянной базой сравнения определим по формуле: ОПД = Текущий показатель / Базисный показатель
Постоянная база сравнения (базисные показатели):
ОПД1 = 2968 / 2453*100% = 120.99%;
ОПД2 = 3326 / 2453 * 100% = 135.59%;
ОПД3 = 3415 / 2453 * 100% = 139.22%.
Проверим взаимосвязь показателей. По свойствам относительных показателей динамики с переменной базой сравнения произведение всех рассчитанных значений должно равняться относительной величине с постоянной базой сравнения. Т.е.: 1.2099*1.1206*1.0268 = 1.3922 = 139.22%. Взаимосвязь подтверждена.
По свойствам относительных показателей динамики с постоянной базой сравнения частное от деления последующего значения показателя динамики с постоянной базой к предшествующим показателем динамики с постоянной базой равняется соответствующему значению показателя динамики с переменной базой сравнения:
1,3559/1,2099 = 1,1206 = 112.06%;
1,3922/1,3559 = 1,0268 = 102.68%.
Взаимосвязь подтверждена.
Задача 6.6
Торговая фирма планировала в 2002 г. по сравнению с 2001 г. увеличить оборот на 14,5%. Выполнение установленного плана составило 102,7%. Определите относительный показатель динамики оборота.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.9
Предприятие планировало увеличить выпуск продукции в 2002 г. по сравнению с 2001 г. на 18%. Фактический же объем продукции составил 112,3% от прошлогоднего уровня. Определите относительный показатель реализации плана.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.11
Имеются следующие данные о внешнеторговом обороте России со странами вне СНГ: (млрд.долл. США)
| 2000 | 2001 | |
|---|---|---|
| Экспорт | 91,3 | 87,7 |
| Импорт | 31,5 | 40,3 |
Вычислите относительные показатели структуры и координации
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.22
Распределение рабочих предприятия по тарифному разряду имеет следующий вид:
| Тарифный разряд | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Число рабочих, чел. | 2 | 3 | 26 | 74 | 18 | 4 |
Определите средний уровень квалификации рабочих предприятия.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.23
Результаты торговой сессии по акциям АО ЛУКойл характеризуются следующими данными:
| Торговая площадка | Средний курс, руб. | Объем продаж, шт. |
|---|---|---|
| Российская торговая система | 446 | 138626 |
| Московская межбанковская валютная биржа | 449 | 175535 |
| Московская фондовая биржа | 455 | 200 |
Рассчитайте средний курс акции по всем трем площадкам вместе взятым.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.24
Имеются следующие данные о реализации одного товара на трех рынках города:
| Рынок | I квартал | II квартал | ||
|---|---|---|---|---|
| Цена за 1 кг., руб. | Продано, т. | Цена за 1 кг., руб. | Реализовано на сумму, тыс.руб. | |
| 1 | 85 | 24 | 95 | 1900 |
| 2 | 75 | 37 | 80 | 2800 |
| 3 | 80 | 29 | 90 | 2070 |
Определите среднюю цену данного товара за I и II кварталы и за полугодие.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.26
Имеются следующие данные о ценах на предлагаемое к продаже жилье в одном из городов.
| Цена за 1 м2, долл. США | Общая площадь, тыс. м2 |
|---|---|
| 300-400 | 29,4 |
| 400-500 | 20,5 |
| 500-600 | 7,3 |
| 600-700 | 7 |
| 700-800 | 4 |
Рассчитайте среднюю цену 1м2 жилья.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.30
Производственная деятельность одного из отделений корпорации за месяц характеризуется следующими данными:
| Предприятие | Общие затраты на производство, тыс.руб. | Затраты на 1 руб. произведенной продукции, коп. |
|---|---|---|
| 1 | 2323.4 | 75 |
| 2 | 8215.9 | 71 |
| 3 | 4420.6 | 73 |
| 4 | 3525.3 | 78 |
Определите средние затраты на 1 руб. произведенной продукции в целом по отделению.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 6.32
Качество продукции предприятия характеризуется следующими данными (за месяц):
| Вид продукции | Процент брака | Стоимость бракованной продукции, руб. |
|---|---|---|
| А | 1,3 | 2135 |
| В | 0,9 | 3560 |
| С | 2,4 | 980 |
Определите средний процент брака в среднем по предприятию.
Эта задача уже решена! Вы можете получить её за 150 руб.
III Блок
Задача 7.4
По результатам зимней экзаменационной сессии одного курса студентов получено следующее распределение оценок по баллам:
| Балл оценки знаний студентов | 2 | 3 | 4 | 5 | Итого |
|---|---|---|---|---|---|
| Число оценок, полученных студентами | 6 | 75 | 120 | 99 | 300 |
Определите:
а) средний балл оценки знаний студентов;
б) модальный балл успеваемости и медианное значение балла;
в) сделайте выводы о характере данного распределения.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 7.6
Распределение торговых фирм по размеру месячного товарооборота характеризуется следующими данными:
| Товарооборот, млн.руб. | До 5 | 5-10 | 10-15 | 15-20 | 20-25 | 25 и более | Итого |
|---|---|---|---|---|---|---|---|
| Число фирм | 20 | 26 | 20 | 14 | 10 | 10 | 100 |
Определите:
а) средний размер месячного товарооборота на одну фирму;
б) модальное и медианное значение месячного товарооборота;
в) сделайте выводы о характере данного распределения.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 7.11
Распределение подростковой преступности по одной из областей РФ за 1-е полугодие 2003 г.:
| Возраст правонарушителей, лет | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Итого |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Количество правонарушителей | 7 | 12 | 13 | 12 | 15 | 24 | 29 | 36 | 42 | 30 | 220 |
Определите показатели вариации:
а) размах;
б) среднее линейное отклонение;
в) среднее квадратическое отклонение;
г) коэффициент вариации.
Оцените количественную однородность совокупности.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 7.13
Распределение длины пробега автофургона торговой фирмы характеризуется следующими данными:
| Длина пробега за один рейс, км. | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Число рейсов за 1 месяц | 20 | 25 | 14 | 18 | 8 | 5 | 90 |
Определите:
а) среднюю длину пробега за один рейс;
б) среднее квадратическое отклонение;
в) коэффициент вариации.
Оцените количественную однородность совокупности.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 7.21
Дисперсия признака равна 10, средний квадрат его индивидуальных значений - 140. Чему равна средняя?
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 7.31
Распределение строительных фирм по объему инвестиций характеризуется следующими данными:
| Объем инвестиций, млн.руб. | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 | Итого |
|---|---|---|---|---|---|---|---|---|
| Число фирм | 4 | 6 | 32 | 34 | 27 | 10 | 7 | 120 |
Определите характеристики распределения:
а) среднюю;
б) моду;
в) среднее квадратическое отклонение;
г) коэффициент вариации и асимметрии.
Сделайте выводы о характере распределения строительных фирм.
Эта задача уже решена! Вы можете получить её за 150 руб.
Контрольная работа №2
IV Блок
Задача 9.6.
По данным задачи 9.2 составьте линейное уравнение регрессии зависимости поступлений по соглашениям по экспорту технологий и услуг технического характера от чистой стоимости предмета соглашений 10 областей РФ в 2003 г. Определите параметры уравнения (а0 и а1). Проанализируйте полученные параметры.
Исходные данные (млн. долл. США)
| Номер области | Чистая стоимость предмета соглашения | Поступления по соглашениям |
|---|---|---|
| 1 | 0,49 | 0,42 |
| 2 | 4,18 | 0,19 |
| 3 | 0,11 | 0,11 |
| 4 | 3,69 | 2,38 |
| 5 | 0,51 | 0,51 |
| 6 | 5,05 | 2,04 |
| 7 | 0,52 | 0,52 |
| 8 | 1,74 | 0,28 |
| 9 | 4,22 | 3,3 |
| 10 | 2,48 | 0,3 |
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 9.9.
Имеются данные о связи между средней взвешенной ценой и объемом продаж облигаций на ММВБ 01.01.2004 г.
| Номер серии | Средняя взвешенная цена, тыс.руб., х | Объем продаж, млрд.руб., у |
|---|---|---|
| A | 84,42 | 79,5 |
| B | 82,46 | 279,7 |
| C | 80,13 | 71,4 |
| D | 63,42 | 242,8 |
| E | 76,17 | 76,3 |
| F | 75,13 | 74,7 |
| G | 74,84 | 210,7 |
| H | 73,03 | 75,1 |
| I | 73,41 | 75,5 |
| J | 71,34 | 335,3 |
Составьте линейное уравнение регрессии. Вычислите параметры и рассчитайте линейный коэффициент корреляции и корреляционное отношение. Сравните величину коэффициента корреляции и корреляционного отношения. Сформулируйте выводы.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 9.15.
Используя данные задачи 9.2, вычислите ранговый коэффициент корреляции Спирмена между числом соглашений и стоимостью предмета соглашений по экспорту технологий и услуг технического характера 10 областей РФ в 2003 г. Сравните полученный результат с результатом задачи 9.8.
| Номер области | Число соглашений | Стоимость предмета соглашения |
|---|---|---|
| 1 | 9 | 0,49 |
| 2 | 7 | 4,19 |
| 3 | 3 | 0,11 |
| 4 | 20 | 3,69 |
| 5 | 8 | 0,51 |
| 6 | 11 | 5,1 |
| 7 | 6 | 0,52 |
| 8 | 13 | 1,75 |
| 9 | 18 | 4,28 |
| 10 | 16 | 2,49 |
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 9.21.
По следующим данным постройте линейное уравнение регрессии, вычислите линейный коэффициент корреляции:
xyсредн = 120, xсредн = 10, yсредн = 10, x2средн = 149, y2средн = 125, Эх = 0,6
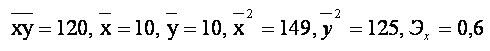
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 9.26.
В ходе проведенного обследования оценки уровня жизни работающих на предприятиях различной формы собственности было опрошено 100 респондентов. Результаты опроса представлены в следующей таблице:
| Форма собственности предприятия | Удовлетворенность уровнем жизни | Итого | |
|---|---|---|---|
| Вполне удовлетворен | Не удовлетворен | ||
| Государственное | 30 | 55 | 85 |
| Частное | 10 | 5 | 15 |
| Итого | 40 | 60 | 100 |
Рассчитайте коэффициенты ассоциации и контингенции. Сформулируйте выводы, вытекающие из анализа полученных коэффициентов.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 9.27.
Распределение предприятий по источникам средств для их покупки характеризуется следующими данными:
| Источник средств | Зарождающийся бизнес | Зрелый бизнес | Итого |
|---|---|---|---|
| Банковский кредит | 31 | 32 | 63 |
| Собственные средства | 38 | 15 | 53 |
| Итого | 69 | 47 | 116 |
Вычислите коэффициенты ассоциации и контингенции. Какие выводы можно сделать на основании значений этих коэффициентов?
Эта задача уже решена! Вы можете получить её за 150 руб.
V Блок
Задача 10.3
Среднесписочная численность работников фирмы в 2003 г. составила: на 1 января - 530 чел., на 1 марта - 570, на 1 июня - 520, на 1 сентября - 430 чел., на 1 января 2004 г. - 550 чел. Вычислите среднегодовую численность работников фирмы за 2003 г.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 10.4
Имеются следующие данные об активах коммерческого банка в одном из регионов за 2003 г. на первое число каждого месяца: (млн.руб.)
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
|---|---|---|---|---|---|---|
| 189 | 190 | 205 | 226 | 208 | 195 | 190 |
Определите среднемесячные уровни активов коммерческого банка за первый, второй кварталы и за полугодие в целом.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 10.5
Остатки вкладов населения в сбербанках города в 2003 г. характеризуются следующими данными на 1-е число месяца. (млн.руб.)
| Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
|---|---|---|---|---|---|---|
| 910.5 | 920.0 | 915.4 | 920.8 | 917.0 | 921.3 | 925.9 |
Определите:
а) среднемесячные остатки вкладов населения за первый и второй кварталы;
б) абсолютный прирост изменения среднего остатка вклада во втором квартале по сравнению с первым.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 10.9
Ввод в действие жилых домов предприятиями всех форм собственности в одном из регионов в 1996 - 2003 гг. характеризуется следующими данными (млн.м2 общей площади):
| 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
|---|---|---|---|---|---|---|---|
| 17 | 18 | 19 | 20 | 21 | 20 | 22 | 23 |
Для анализа ряда динамики 1) определите: цепные и базисные:
а) абсолютные приросты;
б) темпы роста;
в) темпы прироста;
г) среднегодовой темп прироста.
2) найдите для каждого года абсолютное значение 1% прироста;
3) в целом за весь период рассчитайте среднегодовой абсолютный прирост.
Результаты расчетов оформите в таблице и сделайте выводы.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 10.12
Используя взаимосвязь показателей динамики, определите уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным о производстве продукции предприятиями объединения (в сопоставимых ценах):
| Год | Производство продукции, млн.руб. | По сравнению с предыдущим годом | |||
|---|---|---|---|---|---|
| Абсолютный прирост, млн.руб. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн.руб. | ||
| 1998 | 92,5 | ||||
| 1999 | 4,8 | ||||
| 2000 | 104 | ||||
| 2001 | 5,8 | ||||
| 2002 | |||||
| 2003 | 7 | 1,15 | |||
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 10.25
Имеются следующие данные о поголовье коров в хозяйствах всех категорий области. (тыс.голов)
| Дата | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 |
|---|---|---|---|---|---|---|---|---|---|
| На 1 января | 37.6 | 38.1 | 40.1 | 42.5 | - | - | - | - | - |
| На 1 июля | - | - | - | 44.7 | 44.8 | 45.0 | 45.2 | 46.0 | 46.1 |
Установите причину несопоставимости уровней ряда динамики. Приведите уровни ряда к сопоставимому виду.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 10.38 без учета тренда и с учетом
Имеются следующие данные о внутригодовой динамике поставки шерстяных тканей в розничную сеть региона по кварталам 2001 - 2003 гг. (тыс.руб.)
| Квартал | 2001 | 2002 | 2003 |
|---|---|---|---|
| I | 166.1 | 170.8 | 179.9 |
| II | 168.8 | 179.1 | 155.3 |
| III | 191.0 | 171.8 | 186.0 |
| IV | 193.6 | 186.6 | 179.1 |
| Итого | 719.5 | 708.3 | 700.3 |
Для анализа внутригодовой динамики поставки шерстяных тканей:
а) определите индексы сезонности с применением метода аналитического выравнивания по прямой;
б) представьте графически сезонную волну поставки шерстяных тканей по кварталам года и сделайте выводы.
Эта задача уже решена! Вы можете получить её за 150 руб.
VI Блок
Задача 12.2
Рост цен на продовольственные товары в I полугодии 2001 г. в целом по РФ характеризуется следующими данными:
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь |
|---|---|---|---|---|---|---|
| Цена, % к предыдущему месяцу | 103,1 | 102,3 | 101,8 | 102 | 102,3 | 101,9 |
Определите общее изменение цен за весь рассматриваемый период.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.4
Имеются следующие данные о реализации мясных продуктов на городском рынке:
| Продукт | Сентябрь | Октябрь | ||
|---|---|---|---|---|
| Цена за 1 кг, руб. | Продано, ц. | Цена за 1 кг, руб. | Продано, ц. | |
| Говядина | 70 | 26,3 | 80 | 24,1 |
| Баранина | 60 | 8,8 | 60 | 9,2 |
| Свинина | 90 | 14,5 | 95 | 12,3 |
Рассчитайте сводные индексы цен, физического объема реализации и товарооборота, а так же величину перерасхода покупателей от роста цен.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.5
Известны следующие данные о реализации фруктов предприятиями розничной торговли округа:
| Товар | Цена за 1 кг, руб. | Товарооборот, тыс.руб. | ||
|---|---|---|---|---|
| Июль | Август | Июль | Август | |
| Яблоки | 30 | 20 | 143.5 | 167.1 |
| Груши | 40 | 35 | 38.9 | 45.0 |
Рассчитайте сводные индексы:
а) товарооборота;
б) цен;
в) физического объема реализации.
Определите абсолютную величину экономии покупателей от снижения цен.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.6
Определите изменение физического объема реализации потребительских товаров предприятиями розничной торговли города в текущем периоде по сравнению с предшествующим, если товарооборот возрос на 42,3%, а цены повысились на 13,7%.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.7
Объем реализации овощей на рынках города в натуральном выражении в октябре по сравнению с сентябрем возрос на 18,6%, при этом индекс цен на овощную продукцию составил 93,4%. Определите изменение товарооборота.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.9
Деятельность торговой фирмы за два месяца 2003 г. характеризуется следующими данными:
| Товар | Товарооборот, тыс.руб. | |
|---|---|---|
| Март | Апрель | |
| Какао | 54 | 57 |
| Кофе растворимый | 165 | 173 |
| Кофе молотый | 97 | 105 |
| Чай | 80 | 84 |
Определите общее изменение физического объема реализации с учетом того, что в апреле фирма повысила все цена на 3%.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.12
По промышленному предприятию имеются следующие данные:
| Изделие | Общие затраты на производство в 2003 г., тыс. руб. | Изменение себестоимости изделия в 2003 г. по сравнению с 2002 г., % |
|---|---|---|
| Электромясорубка | 1234 | 6 |
| Кухонный комбайн | 5877 | 8,4 |
| Миксер | 980 | 1,6 |
Определите общее изменение себестоимости продукции в 2003 г. по сравнению с 2002 г. и обусловленный этим изменением размер экономии или дополнительных затрат предприятия.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 12.18
Имеются следующие данные о реализации картофеля на рынках города:
| Рынок | Январь | Февраль | ||
|---|---|---|---|---|
| Цена за 1 кг, руб. | Продано, ц. | Цена за 1 кг, руб. | Продано, ц. | |
| 1 | 12 | 24,5 | 14 | 21,9 |
| 2 | 11 | 18,7 | 12 | 18,8 |
| 3 | 10 | 32 | 10 | 37,4 |
Рассчитайте: индекс цен переменного состава; индекс цен фиксированного состава; индекс структурных сдвигов.
Эта задача уже решена! Вы можете получить её за 150 руб.
Кроме представленных имеются и ряд отдельных решенных задач из практикума Р.А. Шмойловой:
Задание 2 из практикума по статистике Р.А. Шмойловой:
По данным приложения 16:
1) произведите группировку 30 коммерческих банков РФ (в зависимости от вашего варианта) по величине: а) кредитных вложений; б) объема вложений в ценные бумаги. К каждой выделенной группе подберите 3-4 наиболее экономически связанных и существенных показателя, имеющихся в таблице, а также вычислите показатели в относительном выражении. Результаты группировки изложите в сводных групповых таблицах и проанализируйте;
2) с помощью аналитической группировки проанализируйте зависимость величины прибыли от других экономических показателей, характеризующих деятельность 30 коммерческих банков. Результаты оформите в таблице. Сделайте выводы;
3) произведите комбинационную группировку 30 коммерческих банков по двум признакам: величине кредитных вложений и объему вложений в ценные бумаги. Проанализируйте полученную группировку.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 5 из практикума по статистике Р.А. Шмойловой:
По данным приложения 16:
1. Постройте ряды распределения по 30 коммерческим банкам РФ: а) по величине прибыли; б) по величине кредитных вложений.
2. По полученным рядам распределения определите: а) прибыль в среднем на один коммерческий банк; б) кредитные вложения в среднем на один коммерческий банк; в) модальное и медианное значение прибыли; г) модальное и медианное значение кредитных вложений.
3. По полученным в п. 1 рядам распределения рассчитайте: а) размах вариации; б) среднее линейное отклонение; в) среднее квадратическое отклонение; г) коэффициент вариации. Необходимые расчеты оформите в табличной форме. Результаты проанализируйте.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 6 из практикума по статистике Р.А. Шмойловой:
Разделив 30 коммерческих банков РФ (задание 2 п.1) на две группы по величине кредитных вложений, выполните следующее:
1. По показателю прибыли рассчитайте: а) общую дисперсию по правилу сложения дисперсий; б) общую дисперсию любым другим способом.
2. Вычислите эмпирическое корреляционное отношение и сделайте выводы.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 3 из практикума по статистике Р.А. Шмойловой:
1. По данным приложения 16 сформулируйте выборочную совокупность, включающую 15-20 коммерческих банков. Вид выборки, метод отбора и алгоритм отбора определите самостоятельно
2. Для сформированной выборочной совокупности вычислите: а) средний объем вкладов граждан; б) среднюю и предельную ошибки выборки (Р=0,954).
3. Определите необходимый объем выборочной совокупности, при котором предельная ошибка будет на 2,5% меньше полученной в п. 2 величины.
4. Сформируйте новую выборочную совокупность рассчитанного в п. 3 объема.
5. Для вновь сформированной выборочной совокупности вычислите: а) средний объем вкладов граждан; б) среднюю и предельную ошибки выборки (Р = 0,954); в) интервал, в котором находится генеральная средняя; г) интервал, в котором находится общий объем вкладов граждан во все банки генеральной совокупности.
6. Вычислите характеристики генеральной совокупности и сравните их с результатами, полученными на основе выборочного наблюдения.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 4 из практикума по статистике Р.А. Шмойловой:
По данным любого статистического ежегодника выполните следующее:
1. выберите интервальный ряд динамики, состоящий из уровней, выраженных абсолютными величинами за 10 периодов подряд (месяцев, лет, кварталов и т. д.).
2. изобразите графически динамику ряда с помощью статистической кривой.
3. по данным этого ряда вычислите абсолютные и относительные показатели динамики. Результаты расчетов изложите в табличной форме и проанализируйте их.
4. вычислите средние показатели динамики и проанализируйте их.
5. произведите сглаживание ряда динамики с помощью скользящей средней и аналитического выравнивания. Расчетные уровни нанесите на график, построенный в пункте 2. Сделайте выводы о характере тенденции рассмотренного ряда динамики.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 8.17 Задача из практикума по статистике Р.А. Шмойловой:
Розничный товарооборот во всех каналах реализации в области увеличился в 2001 г. по сравнению с 2000 г. на 20%, а в 2002 г. по сравнению с 2001 г. - еще на 10%. Определите розничный товарооборот в области в 2000, 2001 и 2002 гг., если абсолютный прирост розничного товарооборота в 2001 г. по сравнению с 2000 г. составил 3600 тыс. руб.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 8.18 из практикума по статистике Р.А. Шмойловой:
В результате опроса каждого пятого учащегося выпускных классов школ района было выяснено, что среднее время, затрачиваемое ежедневно на подготовку к занятиям, составляет 86 мин. при коэффициенте вариации 29,4%. При этом выборочная совокупность составила 128 чел. С вероятностью 0,997 определите границы средних затрат времени на подготовку к занятиям в целом по всем учащимся выпускных классов школ района.
Эта задача уже решена! Вы можете получить её за 150 руб.
Цена консультации по работе Решенные задачи по теории статистики из практикума Р.А. Шмойловой - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:
