22 решенные задачи по статистике на тему Индексы
План (содержание) работы 22 решенные задачи по статистике на тему Индексы:
В данном разделе приведены задачи по статистике по теме "Индексы" с решением.
Задача №1. Расчет среднего индекса цен, индекса товарооборота, взаимосвязь индексов
Имеются данные об объёме товарооборота и изменении цен по отдельным товарным группам:
| Товарные группы | Объём товарооборота в действующих ценах, тыс. руб. | Изменение цен в среднем по группам товаров, % | |
|---|---|---|---|
| Базисный период | Отчётный период | ||
| Швейные изделия: | |||
| Детская одежда | 480 | 560 | -5 |
| Мужская и женская одежда | 1100 | 1250 | 3 |
| Бельё | 200 | 220 | -2 |
| Трикотажные изделия: | |||
| Верхний трикотаж | 650 | 680 | 5 |
| Бельевой трикотаж | 380 | 410 | -4 |
| Чулки-носки | 240 | 260 | -10 |
На основе этих данных определите по отдельным товарным группам и в целом:
1. Индексы цен.
2. Индексы товарооборота в фактических и сопоставимых ценах.
3. Сумму экономии (перерасхода) населения от изменения цен.
Покажите взаимосвязь исчисленных индексов в относительных и абсолютных величинах.
Сделайте экономические выводы.
Решение задачи по статистике индексы №1:
На первом этапе определим индивидуальные индексы цен по отдельным товарным группам. Исходные данные приведены в темпах прироста, поэтому вычисления проведем следующим образом:
ip Детская одежда = (100-5)/100 = 0.95;
ip Мужская и женская одежда = (100+3)/100 = 1.03;
ip Бельё = (100-2)/100 = 0.98;
ip Верхний трикотаж = (100+5)/100 = 1.05;
ip Бельевой трикотаж = (100-4)/100 = 0.96;
ip Чулки-носки = (100-10)/100 = 0.9.
Агрегатный индекс цен характеризует среднее изменение цен по совокупности различных видов продукции и исчисляется по формуле:
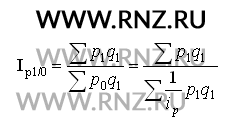
Выполним расчет агрегатного индекса цен для швейных изделий:
Ip1/0 = (560 + 1250 + 220) / (0.95 * 560 + 1.03 * 1250 + 0.98 * 220) = 0.997 или 99,7, то есть в целом по швейным изделиям цены в отчетном периоде снизились на 0,3%
Выполним расчет агрегатного индекса цен для трикотажных изделий:
Ip1/0 = (680 + 410 + 260) / (1.05 * 680 + 0.96 * 410 + 0.9 * 260) = 1.006 или 100,6, то есть в целом по трикотажным изделиям цены в отчетном периоде увеличились на 0,6 %.
Выполним расчет агрегатного индекса цен для всего ассортимента:
Ip1/0 = (1350 + 2030) / (2035,1 + 1341.6) = 1.001 или 100,1, то есть в целом по всему ассортименту товаров цены в отчетном периоде увеличились на 0,1 %.
Фактический товарооборот отчетного года в сопоставимых ценах рассчитывают по формуле:

Составим расчетную таблицу
| Товарная группа | Объём товарооборота в действующих ценах, тыс.руб. | Фактический товарооборот отчетного года в сопоставимых ценах | |
|---|---|---|---|
| Базисный период | Отчётный период | ||
| Детская одежда | 480 | 560 | 589,474 |
| Мужская и женская одежда | 1100 | 1250 | 1213,592 |
| Бельё | 200 | 220 | 224,49 |
| Верхний трикотаж | 650 | 680 | 647,619 |
| Бельевой трикотаж | 380 | 410 | 427,083 |
| Чулки-носки | 240 | 260 | 288,889 |
Вычислим соответствующие индексы:
Швейные изделия: Индекс товарооборота в сопоставимых ценах.
Ip = (560 + 1250 + 220) / (589,474 + 1213,592 + 224,490) = 1.001. Товарооборот швейных изделий за счет изменения цен возрос на 0,1 %.
Абсолютный прирост товарооборота за счет изменения цен:
Δ = 2030 - 2027,556 = 2,444 тыс. руб.
Определим индекс физического объема товарной массы.
Iq = (2027,556) / (480 + 1100 + 200) = 1.139. Вывод. Товарооборот швейных изделий за счет изменения физической массы возрос на 13,9 %.
Абсолютный прирост товарооборота за счет изменения физической массы:
Δ = 2027,556 - 1780 = 247,556 тыс. руб.
Индекс товарооборота в фактических ценах.
Ipq = (560 + 1250 + 220) / (480 + 1100 + 200) = 1.140.
Вывод. Товарооборот швейных изделий за счет изменения двух факторов: цен и физической массы возрос на 14,0 %.
Абсолютный прирост товарооборота за счет изменения этих же двух факторов:
Δ = 2030 - 1780 = 250 тыс.руб.
Выявим взаимосвязи индексов.
В относительном выражении. Полученные значения индексов подтверждают правильность расчетов из соотношения: 1,140=1,139*1,001
Товарооборот в отчетном периоде по сравнению с базисным возрос на 14,0 %, в том числе за счет изменения цен - на 0,01 % и за счет изменения физической массы - на 13,9 %.
Взаимосвязь в абсолютном выражении
Δ = 247,556 + 2,444 = 250 тыс. руб.
Вывод. В абсолютной сумме товарооборот швейных изделий в отчетном периоде по сравнению с базисным возрос на 250 тыс. руб., в том числе за счет изменения цен он возрос на 2,444 тыс. руб. и за счет изменения физической массы - на 247,556 тыс. руб.
Трикотажные изделия. Индекс товарооборота в сопоставимых ценах.
Ip = (680 + 410 + 260) / (647,619 + 427,083 + 288,889) = 0,990. Товарооборот трикотажных изделий за счет изменения цен снизился на 1,0 %.
Абсолютный прирост товарооборота за счет изменения цен
Δ = 1350 - 1363,591 = -13,591 тыс. руб.
Определим индекс физического объема товарной массы.
Iq = (1363,591) / (650 + 380 + 240) = 1,074. Вывод. Товарооборот трикотажных изделий за счет изменения физической массы возрос на 7,4 %. Абсолютный прирост товарооборота за счет изменения физической массы:
Δ = 1363,591 - 1270 = +93,591 тыс.руб.
Индекс товарооборота в фактических ценах.
Ipq = 1350 / 1270 = 1,063 или 106,3 %.
Вывод. Товарооборот трикотажных изделий за счет изменения двух факторов: цен и физической массы возрос на 6,3 %.
Абсолютный прирост товарооборота за счет изменения этих же двух факторов:
Δ = 1350 + 1280 = +80 тыс. руб.
Выявим взаимосвязи индексов в относительном выражении.
Полученные значения индексов подтверждают правильность расчетов из соотношения: 1,063=1,074*0,990
Товарооборот в отчетном периоде по сравнению с базисным возрос на 6,3 %, в том числе за счет изменения физической массы - на 7,4 %, а за счет изменения цен снизился на 1,0 %.
Взаимосвязь в абсолютном выражении:
Δ = 93,591 - 13,591 = +80 тыс. руб.
В целом по ассортименту: Индекс товарооборота в сопоставимых ценах.
Ip = (2030 + 1350) / (2027,556 + 1363,591) = 0,997. Товарооборот в целом по ассортименту за счет изменения цен снизился на 0,3 %. Абсолютный прирост товарооборота за счет изменения цен:
Δ = 3380 - 3391,147 = -11,147 тыс. руб.
Полученная сумма говорит о том, что произошла экономия средств за счет снижения цен на 0,3%. Определим индекс физического объема товарной массы.
Iq = (3391,147) / (1780 + 1270) = 1,112. Вывод. Товарооборот всего ассортимента изделий за счет изменения физической массы возрос на 11,2 %. Абсолютный прирост товарооборота за счет изменения физической массы:
Δ = 3391,147 - 3050 = 341,147 тыс. руб.
Индекс товарооборота в фактических ценах.
Ipq = 3380 / 3050 = 1,108 или 110,8 %
Вывод. Товарооборот за счет изменения двух факторов: цен и физической массы возрос на 10,8 %.
Абсолютный прирост товарооборота за счет изменения этих же двух факторов:
Δ = 3380 - 3050 = 330 тыс. руб.
Выявим взаимосвязи индексов в относительном выражении.
Полученные значения индексов подтверждают правильность расчетов из соотношения: 1,108=1,112*0,997.
Товарооборот в отчетном периоде по сравнению с базисным возрос на 10,8 %, в том числе за счет изменения физической массы - на 11,2 %, а за счет изменения цен снизился на 0,3 %.
Взаимосвязь в абсолютном выражении:
Δ = 341,147 - 11,147 = +330 тыс. руб.
Вывод. В абсолютной сумме товарооборот в отчетном периоде по сравнению с базисным возрос на 330 тыс. руб., в том числе за счет изменения физической массы он возрос на 341,147 тыс. руб., а за счет изменения цен снизился на 11,147 тыс. руб.
Посмотрите больше примеров решения задач по статистике

Задача №2. Расчет индексов скорости товарооборота, индексов времени обращения, взаимосвязи индексов скорости товарооборота и времени обращения
Розничный товарооборот и товарные запасы по предприятию за два квартала составили, тыс. руб.:
| Товарные группы | Товарооборот | Товарные запасы на | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Iкв. | IIкв. | I /I | I / II | I / III | I/ IV | I / V | I / VI | I / VII | |
| A | 180 | 192 | 4,2 | 5,6 | 3,2 | 2,8 | 6,4 | 4,8 | 3,6 |
| B | 105 | 140 | 12,6 | 10 | 14 | 12,4 | 5 | 13,6 | 10,2 |
| ИТОГО: | 285 | 332 | 16,8 | 15,6 | 17,2 | 15,2 | 11,4 | 18,4 | 13,8 |
На основе приведённых данных определите по каждой группе товаров и в целом:
1. Средние товарные запасы по кварталам.
2. Показатели скорости товарооборота и времени обращения за I и II квартал.
3. Индексы скорости товарооборота и времени обращения, установите связь между ними.
Решение задачи по статистике индексы №2:
На первом этапе для расчета необходимых индексов вычислим средние товарные запасы по кварталам. Если имеются данные о товарных запасах за более продолжительный, чем месяц, период времени (например, квартал, полугодие или год) средние товарные запасы вычисляются по формуле:
З = (З1 + З2 + … Зn ) / n, где
З - средние товарные запасы за период больше 1 месяца
n - число дат, на которые зарегистрированы запасы
Средние товарные запасы по кварталам. Товарная группа А:
1 квартал: З1 = (1/2*4,2+5,6+3,2+1/2*2,8)/2 = 4,1 тыс.руб.
2 квартал: З2 = (1/2*2,8+6,4+4,8+1/2*3,6)/2 = 4,8 тыс.руб.
Товарная группа В:
1 квартал: З1 = (1/2*12,6+10,0+14,0+1/2*12,4)/2 = 12,167 тыс.руб.
2 квартал: З2 = (1/2*12,4+5,0+13,6+1/2*10,2)/2 = 9,967 тыс.руб.
Средние товарные запасы в целом:
1 квартал: З1 = (1/2*16,8+15,6+17,2+1/2*15,2)/2 = 16,267 тыс.руб.
2 квартал: З2 = (1/2*15,2+11,4+18,4+1/2*13,8)/2 = 14,767 тыс.руб.
Далее определим показатели скорости товарооборота и времени обращения за I и II квартал.:
 |
 |
 |
Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №3. Расчет индивидуальных индексов цен и физического объёма, общего индекса товарооборота, взаимосвязь между индексами
Имеются следующие данные о реализации товара А торговыми предприятиями района:
| № п/п | Базисный период | Отчётный период | ||
|---|---|---|---|---|
| Количество, т | Стоимость, тыс. руб. | Количество, т | Стоимость, тыс. руб. | |
| 1 | 15 | 45,4 | 18 | 20 |
| 2 | 12 | 26,7 | 15 | 18 |
| 3 | 20 | 68 | 25 | 53 |
Определить:
1. Цену за 1 тонну товара в каждом периоде.
2. Индивидуальные индексы цен и физического объёма.
3. Общие индексы цен и физического объёма.
4. Общий индекс товарооборота в фактических ценах.
5. Показать взаимосвязь между исчисленными индексами.
6. Абсолютный прирост товарооборота за счёт изменения цен по предприятиям и изменения количества проданных тонн продукта.
Решение задачи по статистике индексы №3:
Определим цену за 1 тонну товара в базисном периоде
p1 = 45,4/15 = 3,027 тыс. руб.
p2 = 26,7/12 = 2,225 тыс. руб.
p3 = 68,0/20 = 3,4 тыс. руб.
Определим цену за 1 тонну товара в отчетном периоде
p1 = 20/18 = 1,111 тыс. руб.
p2 = 18/15 = 1,2 тыс. руб.
p3 = 53/25 = 2,12 тыс. руб.
Далее вычисли индивидуальные индексы цен:
ip1 = 1,111 / 3,027 = 0,367 или 36,7%, т.е. в отчетном периоде цены снизились на 63,3%
ip2 = 1,2 / 2,225 = 0,539 или 53,9%, т.е. в отчетном периоде цены снизились на 46,1%
ip3 = 2,12 / 3,4 = 0,624 или 62,4%, т.е. в отчетном периоде цены снизились на 37,6%
Далее вычисли индивидуальные индексы физического объема:
iq1 = 18 / 15 = 1,2 или 120,0%, т.е. в отчетном периоде физический объем увеличился на 20,0%
iq2 = 15 / 12 = 1,25 или 125,0%, т.е. в отчетном периоде физический объем увеличился на 25,0%
iq3 = 25 / 20 = 1,25 или 125,0%, т.е. в отчетном периоде физический объем увеличился на 25,0%
Агрегатный индекс цен характеризует среднее изменение цен по совокупности торговых предприятий и исчисляется по формуле:

Эта задача уже решена! Получите файл за 100 руб.
Задача №4. Расчет индекса средней производительности труда, структурных сдвигов, взаимосвязь между индексами
Имеются следующие данные в товарообороте и затратах труда по трём группам товаров за два периода:
| Наименование товарных групп | Товарооборот тыс., руб. | Среднесписочное число работников, чел. | ||
|---|---|---|---|---|
| Базисный период | Отчётный период | Базисный период | Отчётный период | |
| А | 980 | 805 | 22 | 20 |
| Б | 1320 | 990 | 25 | 18 |
| В | 905 | 1310 | 50 | 53 |
Определите:
1. Индекс среднего уровня производительности труда.
2. Индекс влияния структурных сдвигов в товарообороте на динамику средней производительности труда в неизменной структуре товарооборота.
Покажите взаимосвязь между исчисленными индексами.
Решение задачи по статистике индексы №4:
Рассчитаем среднюю производителньость труда базисного периода: W0 = (980+1320+905)/(22+25+50) = 33.04 тыс.руб.
Рассчитаем среднюю производителньость труда отчетного периода: W1 = (805+990+1310)/(20+18+53) = 34.12 тыс.руб.
Общее изменение среднего уровня производительности труда показывает индекс среднего товарооборота переменного состава.

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №5. Расчет среднего гармонического индекса цен
Имеются по торговому предприятию:
| Товарные группы | Товарооборот в отчетном периоде | Индекс цен |
|---|---|---|
| Ткань хлопчатобумажная | 200.0 | 0.97 |
| Ткань шерстяная | 350.0 | 0.99 |
| Ткань шелковая | 300.0 | 0.95 |
| Ткань льняная | 100.0 | 1.00 |
| Швейные изделия | 800.0 | 0.96 |
| Галантерея | 50.0 | 0.94 |
Определите общее изменение цен в целом по предприятию. Сделайте выводы.
Решение задачи по статистике индексы №5:
Индекс цен определим по формуле: 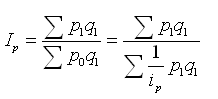
Составим расчетную таблицу:
Эта задача уже решена! Получите файл за 100 руб.

Задача №6. Расчет агрегатного индекса цен
Имеются следующие данные об уценке товаров в отчетном году по универмагу:
| Вид товара | Товарооборот в фактических ценах, тыс.руб. | Изменение розничных цен, % | |
|---|---|---|---|
| Базисный период | Отчетный период | ||
| Обувь на подошве из кожзаменителей | 68.5 | 82.2 | -17.8 |
| Плащи из искусственной кожи | 246.3 | 390.0 | -22.0 |
| Платья детские | 52.3 | 51.1 | -11.0 |
Определите среднее изменение цен на продукцию в целом по магазину. Сделайте вывод.
Решение:
На первом этапе необходимо перевести изменение розничных цен, указанное в %, в десятичные дроби, чтобы получить индивидуальные индексы цен:
iОбувь на подошве из кожзаменителей = (100-17.8)/100 = 0.822.
iПлащи из искусственной кожи = (100-22)/100 = 0.78.
iПлатья детские = (100-11)/100 = 0.89.
Зная индивидуальные индексы цен, определим среднее изменение цен на продукцию в целом по магазину по формуле:
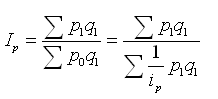
Составим расчетную таблицу:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №7. Расчет индекса затрат на постройку жилья, индекса себестоимости жилья, определение взаимосвязи индексов
Имеются данные по строительным компаниям:
| Строительная компания | Построено жилья, тыс.кв.м. | Себестоимость 1 кв.м., тыс.руб. | ||
|---|---|---|---|---|
| 2006 | 2007 | 2006 | 2007 | |
| 1 | 70 | 85 | 20 | 26 |
| 2 | 90 | 75 | 22 | 28 |
Определите индексы затрат на постройку жилья, индекс себестоимости и индекс физического объема построенного жилья. Показать их взаимосвязь. Найти абсолютное изменение общих затрат на строительство: всего и под влиянием отдельных факторов. Сделать выводы.
Решение:
Составим таблицу вспомогательных расчетов:

Индекс затрат на постройку жилья определим по формуле:

Индекс физического объема построенного жилья определим по формуле:

Эта задача уже решена! Получите файл за 100 руб.
Задача №8. Расчет индивидуальных индексов цен, цепных и базисных индексов цен
По имеющимся данным о средних оптовых ценах на автомобильный бензин в РФ в 2012 г. (табл. 7.6) определите недостающие показатели.
Таблица 7.6. Средние оптовые цены на автомобильный бензин в РФ в 2012 г.
| Месяц | Цена за 1л, руб. | Индивидуальные индексы цен, % | |
|---|---|---|---|
| цепные | базисные | ||
| Апрель | ? | – | 100 |
| Май | 29,5 | ? | ? |
| Июнь | ? | 102,1 | 106,4 |
Решение:
Индивидуальный индекс цен рассчитывается на основе формулы ip = p1 : p0
Цепной индекс цен на июнь можно определить по формуле ip = pиюнь : pмай, соответственно цена 1 л. бензина в июне составит риюнь = ip*рмай = 102.1/100*29.50 = 30.12 руб.

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №9. Расчет сводного индекса товарооборота, сводного индекса цен, сводного индекса физического объема продаж
Известны следующие данные о реализации эмали ПФ предприятиями области (табл. 7.8).
Таблица 7.8. Реализация эмали ПФ предприятиями Орловской области в 2010 г.
| Вид эмали | Цена за 1л, руб. | Товарооборот, тыс. руб. | ||
|---|---|---|---|---|
| июль | август | июль | август | |
| Белая | 88 | 91 | 1608 | 1036,5 |
| Цветная | 94 | 102 | 1701 | 1361 |
Рассчитайте сводные индексы: а) товарооборота; б) цен; в) физического объема реализации. Определите абсолютную величину экономии средств покупателей от снижения цен.
Решение:
Составим таблицу вспомогательных расчетов:

Определим сводный индекс цен:

Эта задача уже решена! Вы можете получить её за 100 руб. 

Задача №10. Определение индекса товарооборота
Объем реализации метизной продукции в натуральном выражении в мае по сравнению с апрелем возрос на 18,6%, при этом индекс цен на метизную продукцию составил 92,4%. Определите изменение товарооборота.
Решение:
Для расчета индекса товарооборота используем формулу взаимосвязи индексов:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №11. Расчет сводного индекса цен, сводного индекса товарооборота, сводного индекса физического объема реализации
Имеются следующие данные о реализации метизной продукции предприятием в августе - сентябре 2010 г. (табл. 7.11).
Таблица 7.11. Реализация продукции ООО Металлснаб в августе - сентябре 2010 г.
| Вид продукции | Товарооборот, тыс.руб. | Изменение цены в сентябре по сравнению с августом, % | |
|---|---|---|---|
| август | сентябрь | ||
| Гвозди | 97 | 63 | 2,1 |
| Гайки | 45 | 40 | 3,5 |
| Болты | 129 | 115 | 4,2 |
Рассчитайте сводные индексы цен, товарооборота и физического объема реализации.
Решение:
На первом этапе необходимо перевести изменение цен, указанное в %, в десятичные дроби, чтобы получить индивидуальные индексы цен:
iгвозди = (100+2.1)/100 = 1.021
iгайки = (100+3.5)/100 = 1.035
iболты = (100+4.2)/100 = 1.042
Зная индивидуальные индексы цен, определим сводный индекс цен по формуле: 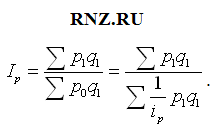
Составим расчетную таблицу:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №12. Расчет индекса цен и перерасхода покупателей
По торговому предприятию имеются следующие данные о реализации стиральных машин (табл. 7.15).
Таблица 7.15. Реализация продукции предприятием в 2010 г.
| Марка стиральной машины | Цена в январе, руб. | Цена в феврале, руб. | Товарооборот февраля, тыс.руб. |
|---|---|---|---|
| А | 12000 | 15500 | 156 |
| Б | 15000 | 19800 | 178 |
| В | 8000 | 8600 | 78 |
Определите: а) средний рост цен на данную группу товаров по торговому предприятию; б) перерасход покупателей от роста цен.
Решение:
На первом этапе рассчитаем индивидуальные индексы цен:
iА = 15500 / 12000 = 1.292.
iБ = 19800 / 15000 = 1.32.
iВ = 8600 / 8000 = 1.075.
Зная индивидуальные индексы цен, определим сводный индекс цен по формуле: 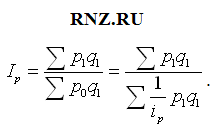
Составим расчетную таблицу:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №13. Расчет индекса себестоимости переменного и постоянного состава, расчет индекса структурных сдвигов
Строительно-производственная деятельность двух ДСК города характеризуется следующими данными (табл. 7.17):
Таблица 7.17
| Домостроительный комбинат | Построено жилья, тыс. кв.м. | Себестоимость 1 кв.м., тыс.руб.с | ||
|---|---|---|---|---|
| 2009 г. | 2010 г. | 2009 г. | 2010 г. | |
| ДСК 1 | 95 | 115 | 29,5 | 31 |
| ДСК 2 | 179 | 107 | 23 | 19,5 |
Рассчитайте индексы: а) себестоимости переменного состава; в) фиксированного состава; в) структурных сдвигов. Объясните результаты расчетов.
Решение:
Составим таблицу вспомогательных расчетов:

Индекс себестоимости фиксированного состава определим по формуле:

Эта задача уже решена! Получите файл за 100 руб.
Задача №14. Расчет общего индекса цен, физического объема продаж, индекса стоимости реализованной продукции
По приведенным ниже данным рассчитайте общие индексы: 1) физического объема товарооборота; 2) цен; 3) стоимости продукции.
Сформулируйте выводы.
| Товар | Индивидуальный индекс цен в августе | Стоимость проданной продукции | |
|---|---|---|---|
| Июль | Август | ||
| Картофель | 98 | 120 | 109 |
| Молоко | 102 | 36 | 38 |
| Яйца | 96 | 132 | 155 |
Решение:
На первом этапе необходимо перевести изменение цен, указанное в %, в десятичные дроби, чтобы получить индивидуальные индексы цен:
iкартофель = 98/100 = 0.98
iмолоко = 102/100 = 1.02
iяйца = 96/100 = 0.96
Зная индивидуальные индексы цен, определим общий индекс цен по формуле: 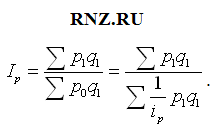
Составим расчетную таблицу:

Эта задача уже решена! Вы можете получить её за 100 руб. 

Задача №15. Расчет общего индекса потребительских цен
Имеются следующие данные о динамике потребительских цен в РФ за 2004 год:
| Товары и услуги | Индекс потребительских цен (2004 г. по отношению к 2003 г.) в разах. | Структура потребительских расходов в 2003 г., % |
|---|---|---|
| Продовольственные товары | 3,2 | 44,9 |
| Непродовольственные товары | 2,8 | 43,1 |
| Платные услуги | 6,9 | 12 |
Требуется рассчитать общий индекс потребительских цен. P.S. Вычисление индекса потребительских цен можно выполнить по формуле среднеарифметической, тождественной агрегатному индексу цен Ласпейреса
Решение:
Расчет ИПЦ можно осуществлять по формуле среднеарифметической, тождественной агрегатному индексу цен Ласпейреса:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №16. Расчет сводного индекса товарооборота, сводного индекса цен, сводного индекса физического объема
Имеются следующие данные о реализации товаров предприятиями розничной торговли:
| Товар | Цена за 1 кг., руб. | Товарооборот, тыс.руб. | ||
|---|---|---|---|---|
| Июнь | Июль | Июнь | Июль | |
| Сахар | 25 | 10 | 220,5 | 300 |
| Соль | 10 | 12 | 78 | 120 |
Рассчитайте сводные индексы: а) товарооборота; б) цен; физического объема реализации.
Ответ представить в виде:
Индекс товарооборота __________________
Индекс цен _____________________
Индекс физического объема ____________________
Взаимосвязь между индексами _________________
Абсолютная экономия покупателей от изменения цен _______________
Решение:
Рассчитаем индивидуальные индексы цен:
iСахар = 10 / 25 = 0.4
iСоль = 12 / 10 = 1.2
Зная индивидуальные индексы цен, определим общий индекс цен:
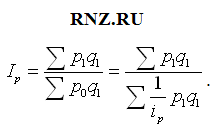
Составим расчетную таблицу:

Эта задача уже решена! Получите файл за 100 руб.
Задача №17. Расчет индивидуальных индексов физического объема, индексный анализ изменения стоимости продукции
За 2014 г. имеются следующие данные:
| Вид продукции | Цена за единицу продукции, руб. | Количество, тыс.шт. | ||
|---|---|---|---|---|
| Апрель | Июнь | Апрель | Июнь | |
| А | 27500 | 28600 | 45 | 50 |
| Б | 20000 | 21100 | 60 | 80 |
Определить:
1. Изменение количества каждого вида продукции, а также изменение количества продукции в целом по предприятию (%).
2. Абсолютное изменение стоимости продукции предприятия, выделив из общей суммы изменение за счет количества продукции и за счет изменения цен.
Решение:
Составим таблицу вспомогательных расчетов:

1. Определим индивидуальные индексы физического объема продаж:
iq1= 50000/45000 = 1.1111
Анализ индивидуального индекса физического объема показывает, что физический объем реализации А увеличился на 11.11% или на 5000 шт.
iq2 = 80000/21100 = 3.7915
Анализ индивидуального индекса физического объема показывает, что физический объем реализации Б увеличился на 279.15% или на 20000 шт.
Для расчета изменения количества продукции в целом по предприятию общий индекс физического объема продукции определим по формуле:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №18. Расчет индекса цен, индексный анализ товарооборота предприятия
Имеются данные о товарообороте продукции по предприятию:
| Наименование | Товарооборот, млн.руб. | Изменение цен в 2014 г. по сравнению с 2013 г. | |
|---|---|---|---|
| 2013 г. | 2014 г. | ||
| А | 1092 | 1360 | +5.3 |
| Б | 1235 | 1582 | +4.3 |
Определить в целом по предприятию:
1. Среднее изменение цен на продовольственные товары (в %);
2. Абсолютное изменение товарооборота розничной торговли за счет изменения цен и физического объема.
Решение:
Составим таблицу вспомогательных расчетов:

Исходя из свойства взаимосвязи индексов, изменение товарооборота за счет увеличения физического объема реализации составило: D(q) = D - D(р) = 615-133.67 = +481.33 млн.руб.
Эта задача уже решена! Вы можете получить её за 100 руб. 

Задача №19. Индексы средней стоимости 1 кв.м. жилой площади, индексный анализ изменения средней стоимости жилья
По муниципалитету имеются следующие данные о стоимости жилой площади:
| Виды жилых домов | Базисный период | Отчетный период | ||
|---|---|---|---|---|
| Стоимость 1 кв.м., у.е. | Количество жилой площади, тыс. кв.м. | Стоимость 1 кв.м., у.е. | Количество жилой площади, тыс. кв.м. | |
| Кирпичные | 530 | 135 | 580 | 186000 |
| Коттеджи | 860 | 62 | 850 | 82000 |
Определите изменение в отчетном периоде по сравнению с базисным по муниципалитету в целом: 1) средней стоимости 1 кв.м. жилой площади; 2) стоимости введенной жилой площади (у.е.) вследствие изменения количества введенной площади. Сформулируйте выводы.
Решение:
Составим вспомогательную таблицу:

Изменение стоимости введенной жилой площади под влиянием изменения количества жилой площади определим посредством анализа агрегатного индекса физического объема реализации, который определим по формуле:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №20. Индексный анализ изменения выработки, объема продукции, численности работников
По строительной фирме имеются следующие данные об изменении объема продукции и численности работников:
| Месяцы | Увеличение (+), снижение (-) по сравнению с предыдущим месяцем | |
|---|---|---|
| Объема продукции | Численности работников | |
| Январь | -2,4 | 2,1 |
| Февраль | 1,6 | -1,4 |
| Март | 5,4 | 1,8 |
| Апрель | 3,2 | 1,1 |
Определите: 1) изменение выработки, объема продукции, численности работников за период январь-апрель месяцы в целом; 2) численность работников за апрель месяц, если в январе численность составила 120 чел. Сформулируйте выводы.
Решение:
Изменение объема продукции за период:

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №21. Индексы себестоимости единицы продукции. Индексный анализ изменения выработки, объема продукции, численности работников
По фирме, производящей железобетонные конструкции известны следующие данные:
| Вид ЖБК | Затраты на производство продукции, тыс.руб. | Изменение себестоимости единицы изделия, % | |
|---|---|---|---|
| Май | Июнь | ||
| Арматура | 680 | 790 | 2,8 |
| Панели перекрытий | 1480 | 1596 | -1.3 |
Определите по фирме в целом изменение в июне по сравнению с маем 1) себестоимости единицы продукции (%); 2) затрат на производство продукции вследствие изменения её себестоимости (тыс.руб.). Сформулировать выводы.
Решение:
Выполним промежуточные вычисления

Эта задача уже решена! Вы можете получить её за 100 руб. 
Задача №22. Расчет индекса затрат
По предприятию затраты топлива на производство единицы продукции в отчетном периоде по сравнению с базисным снизились на 2.6%, производство продукции увеличилось на 8.2%. Определить изменение общих затрат топлива на производство продукции предприятия.
Эта задача уже решена! Вы можете получить её за 100 руб. 
Цена консультации по работе 22 решенные задачи по статистике на тему Индексы - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:
