Решенные задачи по статистике для Института законоведения и управления ВПА, контрольная
План (содержание) работы Решенные задачи по статистике для Института законоведения и управления ВПА:
Задача 3.3.
На основе следующих данных рассчитайте все показатели вариации (дисперсию двумя способами):
| Группы магазинов по величине торговой площади, кв. м | Число магазинов |
|---|---|
| 20-40 | 17 |
| 40-60 | 22 |
| 60-80 | 10 |
| 80-100 | 8 |
| 100-120 | 3 |
Решение оформите в таблице. Объясните экономический смысл полученных результатов. Коэффициент вариации за прошлый период 15 %.
Эта задача уже решена! Вы можете получить её за 150 руб.
Смотрите так же: Решение задач по статистике
Задача 4.3.
Имеются данные о группировке продавцов по уровню производительности труда (оборот на одного работника) за сентябрь отчетного года:
| Товарооборот на 1 продавца, тыс.руб. | Число продавцов, чел. |
|---|---|
| До 10 | 3 |
| 10-15 | 2 |
| 15-20 | 1 |
| 20-25 | 4 |
| Свыше 25 | 5 |
Рассчитайте все показатели вариации (дисперсию двумя способами). Решение оформите в таблице. Объясните экономический смысл полученных результатов. Коэффициент вариации за август 23 %.
Эта задача уже решена! Вы можете получить её за 150 руб.
Приведенные выше задачи по статистике для Института законоведения и управления ВПА решены по следующему образцу:
Методика решения и оформление задач по теме «Показатели вариации»
Задача №3
Имеются следующие данные по продавцам и их стажу работы по торговой фирме «Заря» за отчетный год:
| Группы продавцов по стажу работы, лет | Число продавцов в группе |
|---|---|
| 1-3 | 2 |
| 3-5 | 3 |
| 5-7 | 3 |
| 7-9 | 2 |
Рассчитайте все показатели вариации (дисперсию двумя способами). Решение оформите в таблице. Объясните экономический смысл полученных результатов. Проанализируйте динамику вариации, если коэффициент вариации в прошлом году равнялся 46 %: (Vх0 = 46 % => Кст0 = 100 - 46 = 54 %).
Решение
1. Система показателей вариации:
Размах вариации (разница между максимальным и минимальным значением признака):
Rx = Xmax - Xmin =9 - 1 = 8лет
Среднее значение признака (считается по формуле средней арифметической взвешенной):
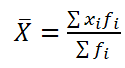= 50 / 10 = 5 лет.
Среднее линейное отклонение (показывает средний разброс индивидуальных значений от среднего показателя без учета направленности по модулю):
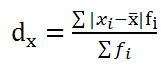= 18 : 10 = 1,8 года; 1 год и 10 мес.
Это означает, что среднее отклонение индивидуального стажа продавцов по отдельным группам работников от среднего стажа в целом по торговой фирме «Заря» в отчетном году без учета знаков отклонение составило 1,8 года.
Дисперсия:
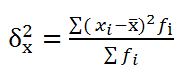= 42 : 10 = 4,2;
= 29,2 - 25 = 4,2;
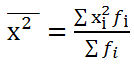= 292 : 10 = 29,2;
Среднее квадратическое отклонение:
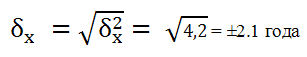
Индивидуальное значение стажа работы продавцов по группам отклоняется от среднего показателя по всему предприятию в пределах ±2,1 года, т.е. границы колеблемости признака в данном случае таковы:
(5 - 2,1) ≤ xi ≤ (5 + 2,1)
2,9 ≤ xi ≤ 7,1.
1.6. Коэффициент вариации - отношение среднего квадратического отклонения к среднему значению признака - показывает, какая часть среднего значения в %-й форме подвержена вариации (колеблемости, испытывает влияние различных факторов).
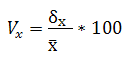= 2.1/5*100 = 40.00 (%)
Это означает, что средний стаж работы в торговой фирме «Заря» в отчетном году варьирует существенно, а именно на 42 % от общего значения. Отсюда закономерно ожидать невысокий показатель однородности продавцов по стажу работы.
1.7. Коэффициент стабильности
Кст = 100 - Vx = 100 - 42.00 = 58,00 (%)
1.8. Анализ динамики вариации:
ΔVx = Vxi - V(x0 = 42.0 - 46.0 = -4.0(%)
ΔKcm = Кст1 - Кст0 = 58.00 - 54.00 = +4.00(%)
Это означает, что совокупность работников за два года по стажу стала более однородной, так как уменьшилась вариация и вырос показатель стабильности на +4,00 %.
2. Проектирование макета таблицы (табл. 3.1):
Таблица 3.1
Исходные и расчетные данные для определения показателей вариации продавцов по стажу работы по торговой фирме «Заря» за отчетный год
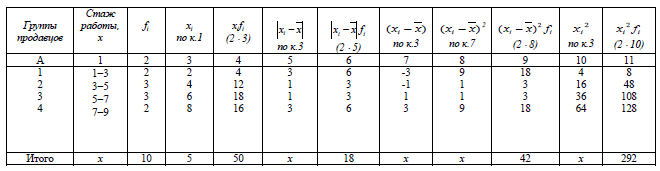
Примечание: Колонка 3 принимается как середина интервала по колонке 1: нижнее значение признака плюс верхнее и разделенное пополам, например (1 + 3) : 2 = 2; (3 + 5) : 2 = 4 и т.д.
Ниже приводится обложка методического пособия, на основе которого были выполнены решенные задачи по статистике для Института законоведения и управления ВПА:
Цена консультации по работе Решенные задачи по статистике для Института законоведения и управления ВПА - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку: