Пример расчета медианы
План (содержание) работы Пример расчета медианы:
Понятие медианы
При анализе различных статистических данных часто возникает необходимость рассчитать различные показатели центра распределения, одним из которых является медиана. Медиана - это один из показателей исследуемого признака, который делит изучаемую совокупность на две равные части, при этом одна часть содержит наблюдения, имеющие значения меньше медианы, а другая состоит из признаков, имеющих значения больше медианного. В силу специфики вычисления медиану считают более достоверной характеристикой типичной величины изучаемого признака, чем, например, средняя арифметическая. Это связано с тем, что рассматриваемый показатель имеет свойство независимости от значений признаков на краях ранжированной совокупности. Нечувствительность к неоднородности изучаемой совокупности и возможным ошибкам выборки при её формировании также называют робастность.
Формула расчета медианы
Применяемая для расчета медианы формула зависит от типа ряда распределения. Например, в неинтервальном ряду с четным количеством наблюдений медиана будет являться средним арифметическим значением из двух центральных величин, т.е. если совокупность состоит из десяти элементов, то искомый показатель будет равняться среднему значению пятого и шестого элемента. В случае, когда ряд неинтервальный и количество наблюдений нечетное, то медианным будет значение признака, находящегося в центре ранжированного ряда, т.е. для 11 элементов это будет шестой элемент.
В интервальном ряду распределения для вычисления медианы используют следующую формулу:
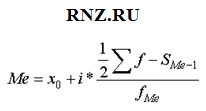
где хО - нижняя граница медианного интервала;
i - ширина медианного интервала;
SМe-1 - накопленная частота интервала, предшествующего медианному;
fМe - частота медианного интервала.
В том случае, если вариационный ряд является дискретным, то медианным будет величина признака в той группе, в которой накопленные частоты превысили половину количества единиц исследуемой совокупности.
Пример расчета медианы в интервальном вариационном ряду
В качестве исходных данных для расчета и анализа медианы используем статистическую группировку банков по величине собственных средств. Таким образом, расчет искомого показателя осуществим на основе следующего интервального ряда распределения:
| № группы | Группы банков по величине собственных средств (капитала) на 01.01.2015, тыс.руб. | Количество банков, ед. |
|---|---|---|
| 1 | 224624-305885 | 2 |
| 2 | 305885-387146 | 11 |
| 3 | 387146-468407 | 5 |
| 4 | 468407-549668 | 5 |
| 5 | 549668-630929 | 3 |
| 6 | 630929-712190 | 4 |
| Итого | 30 |
Для вычисления накопленной частоты построим промежуточную расчетную таблицу:
| № группы | Группы банков по величине собственных средств (капитала) на 01.01.2015, тыс.руб. | Количество банков, ед. | Накопленная частота, S |
|---|---|---|---|
| 1 | 224624-305885 | 2 | 2 |
| 2 | 305885-387146 | 11 | 13 |
| 3 | 387146-468407 | 5 | 18 |
| 4 | 468407-549668 | 5 | 23 |
| 5 | 549668-630929 | 3 | 26 |
| 6 | 630929-712190 | 4 | 30 |
| Итого | 30 | - |
Как показывают проведенные вычисления, середина ряда составляет 15. Следовательно, медианным является интервал с накопленной частой 18. Это интервал со значениями величины собственных средств (капитала) банков на 01.01.2015 в диапазоне 387146-468407 тыс.руб. Соответственно, величина указанного в формуле интервала i равняется 81261 тыс.руб. Нижняя граница требуемого интервала хО составляет 387146 тыс.руб. Накопленная частота интервала, предшествующего медианному, равняется 13.
Соответственно, значение медианы согласно исходным данным составит:
Me = 387146+81261*((30/2-13)/18) = 396175 тыс.руб.
Полученное значение медианы показывает, что в исследуемой совокупности 50% банков имеют величину собственных средств (капитала) более 396175 тыс.руб., а 50% - менее 396175 тыс.руб.
Графический способ определения медианы
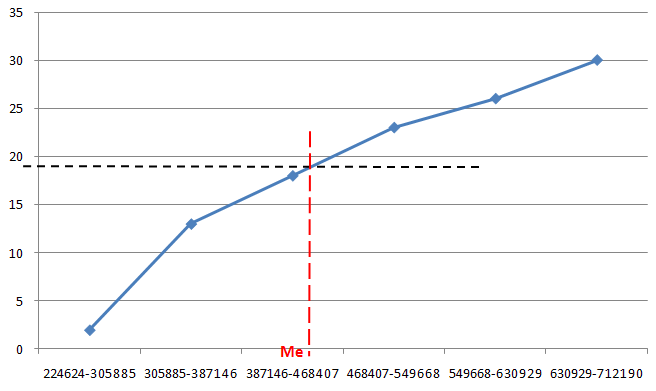
Графически медиана рассчитывается на базе кумуляты. Для её определения из точки на оси накопленных частот (или частостей), соответствующей 50%, строится прямая линия, которая должна быть параллельна оси абсцисс, до пересечения этой линии с кумулятой. Далее из точки пересечения построенной прямой линии с кумулятой строится перпендикуляр на ось абсцисс. Абсцисса точки пересечения и показывает величину медианы.
Больше примеров смотрите на странице Решение задач по статистике
Цена консультации по работе Пример расчета медианы - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:
