Математические модели в экономике, контрольная

Математические модели в экономике, контрольная

ЭММ
Математические модели в экономике

 

Математические модели в экономике, контрольная

План (содержание) работы Математические модели в экономике:

Задача 1

Платёжная матрица игры:

Платёжная матрица игры
Платёжная матрица игры

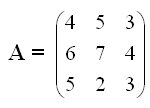
Определить, существует ли седловая точка и найти оптимальное решение.

 

Задача 2

Платёжная матрица игры задана в виде:

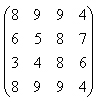
Платёжная матрица игры
Платёжная матрица игры

Упростить игру (упростить платёжную матрицу) и найти оптимальное решение.

 

Задача 3

Найти решение матричной игры:

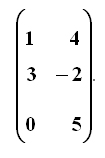
Матричная игра
Матричная игра

 

Задача 4

Оптимально спланировать выпуск продукции при разных состояниях природы - рынка спроса

Предприятие может выпускать 4 вида продукции: A1, A2, A3, A4, получая при этом прибыль. Её величина определяется состоянием спроса (природой рынка), который может находиться в одном из четырёх возможных состояний: B1, B2, B3, B4. Зависимость величины прибыли от вида продукции и состояния рынка представлено в таблице:

Виды продукции
Возможные состояния рынка спроса
B1
B2
B3
B4
A1
4
3
5
6
A2
2
6
1,75
5
A3
3,5
3
7
2
A4
3
5
1,5
3

 

Задача 5

Решить транспортную задачу:

Запасы на терминалах
Запросы предприятий
П1=70
П 2=120
П 3=160
П 4=140
Т1=130
4
7
2,9
3
Т 2=190
3,2
3,5
2,7
4
Т 3=250
5
6
3
7

 

Задача 6

Рассматривается экономическая система, состоящая из трёх отраслей. Назовём их условно: топливно-энергетическая отрасль, промышленность и сельское хозяйство. Пусть матрица В.Леонтьева:

0.1
0.1
0.3
А =
0.3
0.5
0.2
0.4
0.3
0.1

v = (4; 10; 4) - матрица норм добавленной стоимости.

Определим равновесные цены и вектор полных затрат.

 

Задача 7

Структурная матрица торговли 4-х стран:

0.4
0
0.2
0.5
А =
0.5
0.7
0
0
0
0.2
0.3
0
0.1
0.1
0.5
0.5

Найти бюджетный вектор бездефицитной торговли 4-х стран, если суммарный вектор бюджетов составляет 5 триллионов у.е.

 

Задача 8

Решить следующую задачу ЛП в неканонической форме симплекс-методом:

f(x) = x1-x2-3x3 -> min

при ограничениях:

2x1-x2+x3 <= 1

4x1-2x2+x3 >= -2

2x1+x3 <= 5

x1, x2, x3 >= 0

 

Задача 9

Составить матрицу Леонтьева, определить её продуктивность

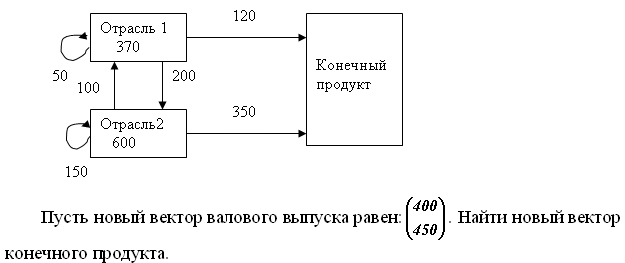
Пусть новый вектор валового выпуска равен: (400; 450). Найти новый вектор конечного продукта

Задача 10

Определить на ПК запас продуктивности матрицы А

0.36
0.15
0.23
0.32
А =
0.22
0.11
0.132
0.356
0.13
0.21
0.02
0.175
0.154
0.217
0.124
0.213

 

Цена консультации по работе Математические модели в экономике - договорная.

Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку: