Контрольная по теории вероятности N0004
Контрольная по теории вероятности N0004
План (содержание) работы Контрольная по теории вероятности N0004:
Задача 19.
В следующей задаче составить ряд распределения дискретной случайной величины, построить многоугольник распределения, найти функцию распределения и построить е график, вычислить математическое ожидание, дисперсию, среднее квадратичное отклонение и найти вероятность того, что случайная величина Х принимает значение, большее своего математического ожидания.
В лотерее 100 билетов, из них 20 выигрышных. Некто купил 3 билета. Случайная величина Х - число выигрышных билетов.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 49.
Непрерывная случайная величина задана своей плотностью вероятности (нечетные номера) или своей функцией распределения (четные номера). Используя свойства плотности вероятности или функции распределения случайной величины Х соответственно найти коэффициент а, найти для нечетных номеров: функцию распределения, для четных номеров: плотность вероятности, построить графики плотности и функцию распределения; найти числовые характеристики и вероятность того, что случайная величина Х принимает значения, отстоящие от своего математического ожидания не более чем на удвоенное среднее квадратичное отклонение.
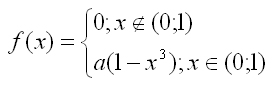
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 79 а).
Случайная величина Х имеет биномиальное распределение с параметрами n=6 и p=0,1. Составить ряд распределения, построить многоугольник распределения, найти функцию распределения и построить ее график, вычислить числовые характеристики: математическое ожидание, моду, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и эксцесса и найти P(X>M).
Задача 79 б).
Случайная величина Х имеет распределение Пуассона с параметром a=1. Составить ряд распределения и построить его график. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение, коэффициенты асимметрии и найти вероятность того, что случайная величина Х принимает положительные значения.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 109.
Рассматриваются три случайные величины, имеющие соответственно равномерное, показательное и нормальное распределение с одним и тем же математическим ожиданием М = 1,24 и с одинаковой дисперсией D = 1,54. Написать выражение плотности для каждой случайной величины и построить их кривые распределения. Найти функции распределения и построить их графики. Найти вероятности того, что каждая из них попадет на интервал, отстоящий в ту или другую сторону от математического ожидания на единицу, и оставаясь при этом положительной. Сделать заключение, какая из них наиболее вероятно попадет на этот интервал, а какая наименее вероятно.
Эта задача уже решена! Вы можете получить её за 150 руб.
Задача 139.
Задана двумерная дискретная случайная величина (X,Y) (двумерный случайный вектор дискретного типа) своей таблицей распределения. Найти:
а) функцию распределения F(x,y) и функции F1(x) и F2(y) и выяснить зависимы или независимы случайные величины Х и У;
б) условные законы распределения;
в) числовые характеристики;
г) коэффициент корреляции;
д) условное математическое ожидание;
е) корреляционные отношения и сравнить их с квадратом коэффициента корреляции.
| У/Х | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|
| 4 | 0,15 | 0,06 | 0,25 | 0,04 | 0,5 |
| 7 | 0,3 | 0,1 | 0,03 | 0,07 | 0,5 |
| 0,45 | 0,16 | 0,28 | 0,11 | 1 |
Эта задача уже решена! Вы можете получить её за 150 руб.
Цена консультации по работе Контрольная по теории вероятности N0004 - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:
