Контрольная по теории вероятности N0002
Контрольная по теории вероятности N0002
План (содержание) работы Контрольная по теории вероятности N0002:
Задание 1
Вопрос 1. Каким событием согласно терминологии теории вероятностей является попадание в мишень при выстреле в тире?
1) Достоверным событием
2) Возможным событием
3) Событием, совместимым с событием А, если событие А состоит в непопадании в мишень
4) Событием противоположным событию А, если событие А состоит в попадании в мишень
Вопрос 2. Предположим, что событие А при проведении испытаний имело место раз. Какова абсолютная частота появления события А?
1. (k-s)/k
2. s/k*100%
3. s/k
4. s
5. M = k/s
Вопрос 3. При шести бросаниях игральной кости (кубика с цифрами от 1 до 6 на гранях) цифра 5 выпала 2 раза, цифра 4 выпала 2 раза, а цифры 3 и 2 выпали по 1 разу каждая. Какова по результатам этого наблюдения частность (относительная частота) события, состоящего в выпадении цифры 3 или цифры 4?
1. 1/6
2. 1/3
3. 1/2
4. 2/3
5. 3/5
Вопрос 4. Каково статистическое определение вероятности?
1. Вероятностью события А называется отношение числа исходов, благоприятствующих событию А, к общему числу испытаний в серии наблюдений;
2. Вероятностью называют устойчивую частоту появления события;
3. Вероятностью называют постоянную величину, около которой группируются наблюдаемые значения частости;
4. Вероятностью называют среднее арифметическое частости появления события при проведении серии одинаковых испытаний;
5. Вероятностью называют отношение числа благополучных исходов к числу всех равновозможных исходов.
Вопрос 5. Какое событие является достоверным?
1. Событие, которому благоприятствуют более половины из единственно возможных исходов испытания
2. Выпадение положительного числа при падении игральной кости
3. Извлечение вслепую белого шара из урны, в которой находятся одинаковые, за исключением цвета, белые и черные шары
4. Падение бутерброда маслом вверх
5. Выпадение разных цифр при двух бросаниях игральной кости
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 2
Вопрос 1. В каком случае система событий E1, E2, … En называется полной
1. Если сумма вероятностей этих событий равна единице
2. Если события E1, E2, … En несовместны и равновозможны
3. Если произведение вероятностей этих событий равно единице
4. Если события E1, E2, … En являются несовместимыми и единственно возможными
5. Если сумма вероятностей этих событий превышает единицу, а сами события являются совместимы
Вопрос 2. Допустим, что при некотором испытании возможны события А и В, вероятность события А P(A) = p, вероятность события В P(B) = 1-p. Какое из приведенных ниже высказываний не всегда будет истиной?
1. Событие А является противоположным событию В
2. Событие В является противоположным событию А
3. Если события А и В являются единственно возможными, то система событий А, В является полной
4. События А и В - равновозможные
5. Событие, которое благоприятствуют А и В является достоверным
Вопрос 3. Какова вероятность того, что при трех бросаниях игральной кости три раза выпадет цифра 3?
1. 1/6
2. 1/2
3. 1/216
4. 1/36
5. 1/72
Вопрос 4. Из урны, в которой 4 белых шара и 3 черных, случайным образом извлекают два шара. (Шар после извлечения не возвращают в урну). Шары в урне различаются только цветом. Какова вероятность того, что первым будет извлечен черный шар, а вторым - белый?
1. 13/42
2. 2/7
3. 1/49
4. 2/49
5. 1/42
Вопрос 5. При попадании в мишень пули, она опрокидывается. Допустим, что о стрелке А известно, что он попадет в мишень с вероятностью 4/5, о стрелке В известно, что он попадет в мишень с вероятностью 1/3, а о стрелке С известно, что он попадет в мишень с вероятностью 3/4. Стрелки А, В, С одновременно выстрелили в мишень. Какова вероятность того, что мишень опрокинется?
1. 1/5
2. 4/5
3. 29/30
4. 11/15
5. 51/60
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 3
Вопрос 1. Что выражает формула Бернулли?
1.Теорему сложения вероятностей
2. Вероятность появления события r раз при k независимых испытаниях (k > r > 0)
3. Вероятность появления события А в двух независимых испытаниях
4. Вероятность появления двух совместных событий при одном испытании
5. Условную вероятность единственно возможного события
Вопрос 2. Какова вероятность того, что 4 раза извлекая из урны, с завязанными глазами шар, мы ровно 2 раза извлечем белый, если в урне 6 белых шаров и 4 черных, и после каждого извлечения шар возвращается в урну?
1. 0.36*0.96
2. 0.5
3. 0.1
4. 0.36
5. 0.16
Вопрос 3. Для определения какой величины служит формула Байеса?
1. Для определения события Аi, противоположного событию E
2. Для определения полной вероятности события Аi
3. Для определения вероятности события Аi при условии появления события Е
4. Для определения вероятности появления события Аi или Е
5. Для определения вероятности появления в ряду независимых испытаний события Е после события Аi.
Вопрос 4. Стрелок попадает в цель с вероятностью 0,6. Каково для этого стрелка наиболее вероятное число попаданий в цель при 6 выстрелах?
1. 2
2. 3
3. 4
4. 5
5. 6
Вопрос 5. Вероятность изготовления годного изделия автоматическим станком равна 0,9. Вероятность изготовления изделия первого сорта этим станком равна 0,8. Какова вероятность того, что случайно взятое из годных, изделие окажется первого сорта?
1. 8/9
2. 0.72
3. 0.8
4. 0.6
5. 0.98
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 4
Вопрос 1. Что называется кривой вероятностей?
1. График зависимости вероятности попадания в цель от расстояния до цели
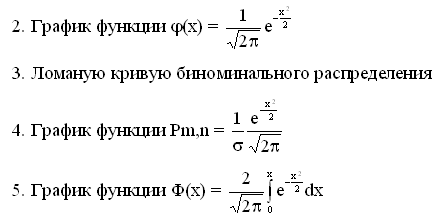
Вопрос 2. Для чего применяется локальная теорема Лапласа?
1. Для приближенного определения вероятности появления события m раз при n повторных независимых испытаниях;
2. Для отыскания максимума кривой вероятностей
3. Для отыскания точки пересечения кривой вероятностей φ(х) с осью Ох
4. Для отыскания минимума кривой вероятностей
5. Для статистического анализа результатов повторных независимых испытаний.
Вопрос 3. Как выглядит асимптотическая формула Пуассона?
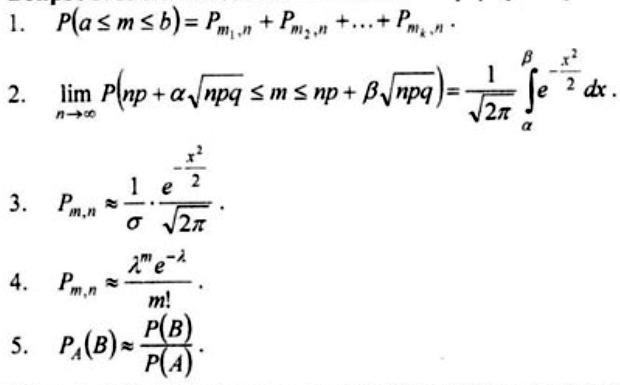
Вопрос 4. При каком условии допустимо использование асимптотической формулы Пуассона?
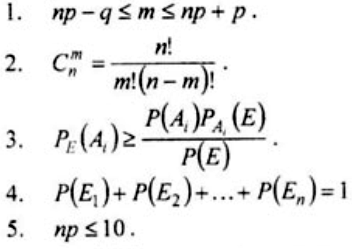
Вопрос 5. Пусть n - число независимых испытаний, в каждом из которых вероятность наступления события А равна p. Чему равен предел вероятности того, что число m появления события А при n испытаниях удовлетворяет неравенству np+a√npq ≤ m ≤ √npq, если n неограниченно возрастает?
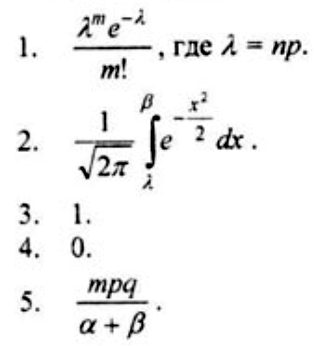
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 5
Вопрос 1. В каком случае говорят, что дискретная случайная величина Х, у которой возможных значений определена?
1. Если известен исход испытания, определяющего значения случайной величины Х
2. Если известны все k возможных значений случайной величины Х
3. Если известны (заданы) все возможные значения х1, х2, … хk случайной величины и соответствующие вероятности Р(х1) = рi
4. Если заданы k значений вероятностей исхода испытания
5. Если заданы минимальное и максимальное значения случайно величины Х
Вопрос 2. Что называют функцией распределения непрерывной случайной величины Х?
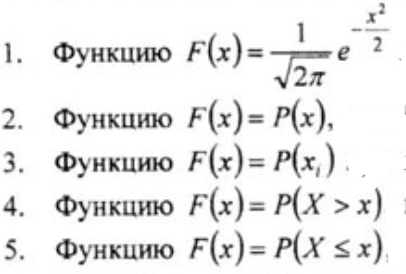
Вопрос 3. Каким свойством не обладает интегральная функция распределения F(x)?
1. 0 ≤ F(x) ≤ 1
2. F(-∞) = 0
3. F(∞) = 1
4. F(х) - непрерывна
5. F(х) - невозрастающая
Вопрос 4. Чему равна плотность распределения вероятностей случайной величины Х, удовлетворяющей условию a < X < b и равномерно распределенной на интервале (a;b), если a>0, b ≠ a.
1. (b-a)/x
2. (b-a)*x
3. 1/(b-a)
4. υ (х) = x
5. F'(х) = 1/x
Вопрос 5. График какой функции называют кривой распределения вероятностей непрерывной случайной величины Х?

Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 6
Вопрос 1. Каково среднее значение случайной величины, принимающей значение 1 с вероятностью 0,25 и значение 3 с вероятностью 0,75?
1. 2
2. 1,25
3. 1,5
4. 2,5
5. 1,75
Вопрос 2. Чему равно математическое ожидание M(X+Y) суммы двух случайных величин X, Y?
1. M(X+Y) = M(X)*M(Y)
2. M(X+Y) = M(X)+M(Y)
3. M(X+Y) = (M(X)+M(Y))/2
4. M(X+Y) = M(X)+2M(XY)+ M(Y)
5. M(X+Y) = (x2+y2)/4
Вопрос 3. В каком случае можно утверждать, что математическое ожидание M(X*Y) произведения двух случайных величин X, Y равно произведению их математических ожиданий M(X)*M(Y)?
1. Если случайные величины X и Y - дискретные;
2. Если случайные величины X и Y - непрерывные;
3. Если плотность распределения φ(X * Y) - непрерывная функция;
4. Если количество значений, принимаемых случайной величиной Х совпадает с количеством значений, принимаемых случайной величиной Y
5. Если случайные величины X и Y - независимы.
Вопрос 4. Что называют дисперсией случайной величины?
1. Среднеквадратическое отклонение случайной величины.
2. Среднее значение отклонения случайной величины от 0;
3. Среднее значение отклонения случайной величины от её математического ожидания;
4. Среднее значение квадрата отклонения случайной величины от её математического ожидания;
5. Модуль максимального отклонения значение случайной величины от её математического ожидания.
Вопрос 5. Чему равна дисперсия D(X+Y) суммы независимых случайных величин X, Y?
1.|D(X)-D(Y)|
2. M((X+Y)-(M(X)+M(Y))2)
3. M((X+Y) - M(X) - M(Y))2)
4. √ D(X)*D(Y)
5. D(X)*D(Y)/2
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 7
Вопрос 1. Каково среднее значение случайной величины, если плотность ее вероятности определяется формулой:
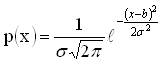
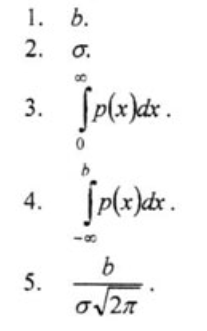
Вопрос 2. Как формулируется теорема Ляпунова?

Вопрос 3. Какие два параметра однозначно определяют случайную величину, подчиненную нормальному закону распределения?
1. Среднее квадратическое отклонение и дисперсия
2. Математическое ожидание и дисперсия
3. σ, е
4. М(Х), π
5. Максимальное значение функции плотности вероятности и среднее квадратическое отклонение.
Вопрос 4. Рассмотрим непрерывную положительную случайную величину Х с математическим ожиданием M(X) = 3. Что можно утверждать относительно вероятности P(X)≤ 4 на основании неравенства Маркова?
1. P(X≤ 4) ≤ D(X)
2. P(X ≤ 4) > D(X)
3. P(X ≤ 4) ≥ 0.25
4. P(X ≤ 4) > 0.75
5. P(X ≤ 4) ≤ 0.75
Вопрос 5. Рассмотрим случайную величину Х, математическое ожидание которой равняется 0, а дисперсия - 10. Как оценивается P(|X|>10), исходя из неравенства Чебышева?
1. P(|X|>10) ≥ 0.1
2. P(|X|>10) < 1
3. P(|X|>10) ≥ 0.01
4. P(|X|>10) < 0.1
5. P(|X|>10) < 0.01
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 8
Вопрос 1. Пусть вероятность появления события А в отдельном испытании составляет 0,7 и мы подсчитываем число m появления события А в n таких независимых испытаниях. При каком числе испытаний n вероятность выполнения неравенства |m/n - 0.7| < 0.25 превысит 0,9?
1. n = 18
2. n < 142
3. n ≥ 34
4. n ≥ 24
5. n ≥ 41
Вопрос 2. Проверено 3000 патронов из всего их выпуска. При этом доля брака составила 0,15. Какова вероятность того, что отклонение доли брака в выборке от генеральной доли не превышает по абсолютной величине 0,01? (выборка повторная)
1. P = 0.53262
2. P = 0.87398
3. P = 0.80640
4. P = 0.72429
5. P = 0.57629
Вопрос 3. По данным выборки, представленным вариационным рядом:
| x | 1 | 2 | 5 | 8 | 9 |
|---|---|---|---|---|---|
| частоты | 3 | 4 | 6 | 4 | 3 |
найти выборочную среднюю x и выборочную дисперсию и выбрать правильный ответ:
1. x = 5, S2 = 12.5
2. x = 4, S2 = 10
3. x = 25, S2 = 25
4. x = 4, S2 = 8.5
5. x = 5, S2 = 8.84
Вопрос 4. Для каждой из 1500 независимых случайных величин дисперсия не превышает 3. Какова вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий не превысит числа 0,4 по абсолютной величине? (Используйте теорему Чебышева)
1. P > 0.9925
2. P > 0.9875
3. P > 0.9233
4. P > 0.9548
5. P > 0.8732
Вопрос 5. По данным ОТК брак при выпуске деталей составляет 2,5%. Пользуясь теоремой Бернулли, ответьте на вопрос: какова вероятность того, что при просмотре партии из 8000 деталей будет установлено отклонение от средней доли брака менее 0,005?
1. P > 0.878125
2. P > 0.43512
3. P > 0.63285
4. P > 0.53485
5. P > 0.93248
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 9
Вопрос 1. При каком объеме выборки можно утверждать с надежностью P=0.9545, что отклонение выборочной средней от генеральной не превысит предельной ошибки Δ = 0.25 при повторной выборке, если дано σ = 1?
1. n = 8
2. n = 64
3. n = 12
4. n = 16
5. n = 82
Вопрос 2. Для данных выборочного наблюдения n = 64, x = 36.41 и sn = 1 каков будет доверительный интервал для оценки M(x) = a с надежностью P = 0.9973.
1. 36.035 ≤ a ≤ 36.785
2. 32.015 ≤ a ≤ 32.240
3. 36.16 ≤ a ≤ 36.66
4. 30.035 ≤ a ≤ 30.075
5. 33.15 ≤ a ≤ 33.45
Вопрос 3. Что означает большая теснота корреляционной зависимости величин х и у?
1. Наличие линейной корреляции между х и у
2. Большую степень рассеяния значений у относительно значений х
3. Отсутствие функциональной зависимости между х и у
4. Малую степень рассеяния значений у относительно линии регрессии
5. Наличие точной корреляционной зависимости между х и у
Вопрос 4. Что определяет уравнение регрессии у по х?
1. Функциональную зависимость у от среднего значения х
2. Плотность распределения переменной у
3. Тесноту корреляционной зависимости у от х
4. Зависимость частных средних значений у (при определенных х) от х
5. Степень линейности зависимости между у от х
Вопрос 5. По какому набору данных можно определить предельную ошибку выборки?
1. Объем выборки, выборочная средняя, заданная надежность
2. Объем генеральной совокупности, выборочная средняя, объем выборки
3. Заданная надежность, выборочная средняя, выборочная дисперсия
4. Объем генеральной совокупности, заданная надежность, выборочная средняя, выборочная дисперсия
5. Объем выборки, заданная надежность, выборочная дисперсия
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 10
Вопрос 1. Какое из следующих утверждений неверно? Линейная функциональная зависимость между х и у имеет место при:
1. Слиянии прямых регрессии у по х и х по у
2. Равенстве коэффициент корреляции ± 1
3. Равенстве коэффициента корреляции 0
4. Расположении частот значений х и у лишь на одной диагонали корреляционной таблицы
5. Равенстве единице произведения коэффициентов прямых регрессии у по х и х по у
Вопрос 2. Как выглядит график прямых регрессий при условии ρ x/y>0; ρ y/x>0?
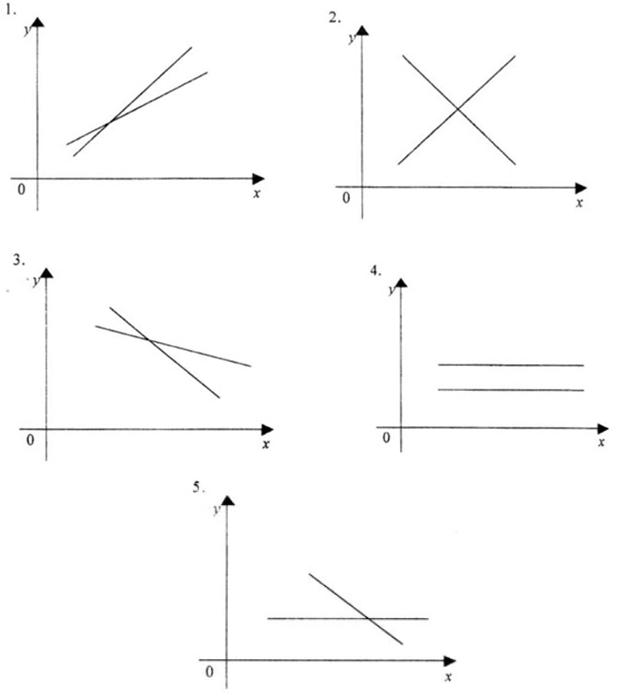
Вопрос 3. Чему равен коэффициент корреляции двух случайных независимых величин х и у, если xсреднее = 4, yсреднее = 2, σ х = 2, σ y = 4.
1. 1
2. 0,5
3. -0,5
4. 0
5. -1
Вопрос 4. Чему равен коэффициент корреляции r случайных величин х и у, полученный на основании данных таблицы?
| o o | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | nx |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 5 | 10 | 2 | - | - | - | - | 20 |
| 3 | 4 | 5 | 8 | 5 | 2 | 1 | - | - | 25 |
| 4 | - | 3 | 2 | 6 | 5 | - | 1 | - | 17 |
| 5 | 3 | 2 | 3 | 2 | 8 | 1 | - | - | 19 |
| 6 | - | - | - | 2 | 2 | 3 | 2 | 1 | 10 |
| ny | 10 | 15 | 23 | 17 | 17 | 5 | 3 | 1 | 91 |
1. 0,82
2. 0,54
3. 0,21
4. 0,03
5. 0,99
Вопрос 5. Чему равны коэффициенты регрессии ρ x/y; ρ y/x случайных величин х и у, представленных таблицей из вопроса 4?
1. 0,25 и 0,75
2. 0,15 и 0,35
3. 0,82 и 0,48
4. 0,45 и 0,65
5. 0,93 и 0,35
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 11
Вопрос 1. При обследовании 11 учеников получены следующие данные о росте и весе:
| Вес (кг), У Рост (см), Х | 24 | 25 | 26 | 27 | nx |
|---|---|---|---|---|---|
| 125 | 1 | - | - | - | 1 |
| 126 | 1 | 2 | - | - | 3 |
| 127 | - | 2 | 4 | 1 | 7 |
| ny | 2 | 4 | 4 | 1 | 11 |
Чему равен коэффициент корреляции роста и веса учеников?
1. 0.23
2. 0.98
3. 0.15
4. 0.35
5. 0.67
Вопрос 2. Какое из следующих утверждений, связывающий корреляционное отношение η и коэффициент корреляции r неверно?
1. η у/х > r при точной линейной корреляционной связи у по х
2. η ≥ r
3. η ≤ r
4. η х/у = r при точной линейной корреляционной связи х по у
5. η х/у = η у/х = r при точной линейной корреляционной связи и х по у и у по х.
Вопрос 3. Данные статистической обработки сведений по двум показателям х и у отражены в корреляционной таблице. Чему равен коэффициент корреляции?
| х у | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|
| 1 | 2 | - | - | - | - |
| 2 | - | 1 | - | - | - |
| 3 | - | - | 5 | - | - |
| 4 | - | - | - | 3 | - |
| 5 | - | - | - | - | 4 |
Чему равен коэффициент корреляции?
1. 0
2. 0.9
3. 1
4. 0.4
5. 0.5
Вопрос 4. На графике изображена прямая регрессия х по у. Чему равен коэффициент регрессии ρ x/y?
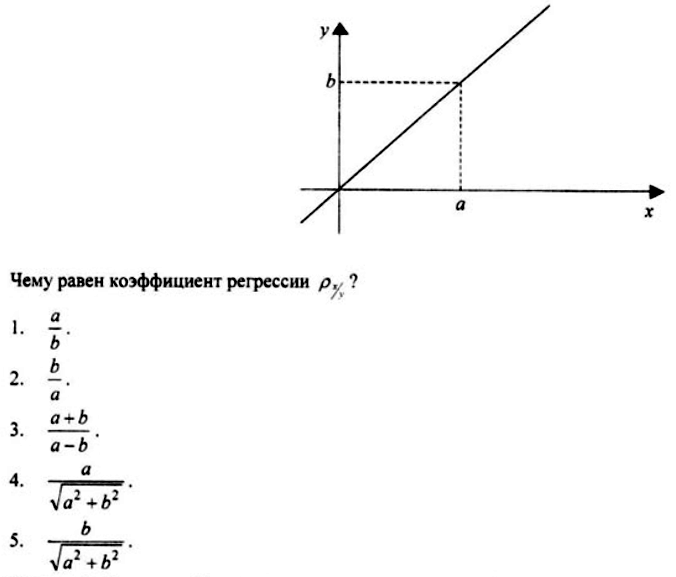
Вопрос 5. Какие преобразования нужно произвести, чтобы перейти от переменных х, у к переменным n, v, представленным в таблицах

Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 12
Вопрос 1. Что называют пространством выборок?
1. Генеральную совокупность (множество), которому принадлежат результаты наблюдений
2. Числовую таблицу наблюдений случайной величины
3. Множество значений вероятностей исхода испытаний
4. Множество рациональных чисел
5. Множество действительных чисел, из которого выбран результат наблюдения
Вопрос 2. Что такое статистическая гипотеза?
1. Предположение о распределении вероятностей или о некотором множестве распределения вероятностей
2. Предположение о результате наблюдения
3. Предположение о пространстве выборок
4. Предположение, которое может быть строго доказано на основании анализа результатов конечного числа наблюдений (испытаний)
5. Суждение о правдоподобии статистических данных.
Вопрос 3. Какова роль уровня значимости при проверке гипотез. Как он используется?
1. Если параметры двух событий отличаются на величину менее ε t, то события считаются одинаковыми (равными)
2. Событие считается практически невозможным, если его вероятность меньше ε
3. Если величина критического события А для гипотезы Н превосходит ε , то ε называют гарантированным уровнем значимости критерия А для Н
4. Если вероятность двух событий отличается меньше, чем на ε , то события считают практически равновероятными
5. Гипотеза Н отвергается на уровне значимости ε , если в эксперименте произошло событие А, вероятность которого при гипотезе Н превосходит ε.
Вопрос 4. Что называют ошибкой второго рода?
1. Погрешность вычисления математического ожидания
2. Ошибку при выборе гарантированного уровня значимости
3. Ошибку при формировании критического множества
4. Отвержение гипотезы в случае, если она верна.
5. Принятие (неотвержение) гипотезы, если она неверна.
Вопрос 5. Какая схема является статистической моделью тройного теста (теста дегустатора)?
1. Схема алгоритма Евклида
2. Схема Ферма
3. Схема Пуассона
4. Схема Бернулли
5. Схема Блэза Паскаля
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 13
Вопрос 1. Какова левосторонняя альтернатива гипотезы Н: р = 1/5 при тройном тесте?
1. Н1 : р ≠ 1/3
2. Н1 : р < 1/3
3. Н1 : р > 1/5
4. Н1 : р < 1/5
5. Н1 : р > 1/3
Вопрос 2. Как определяется уровень значимости для тройного теста, если разумная альтернатива к гипотезе Н0 : р = р0 (р0 - фиксированное число) является двусторонней, т. е. Н0 отвергается, если Sнабл ≤ y или Sнабл ≥ х?
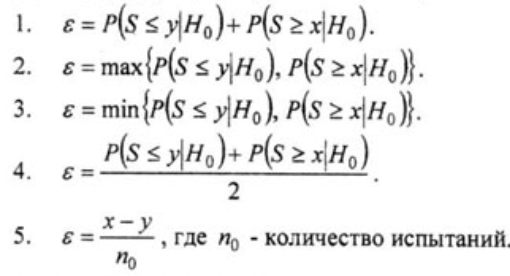
Вопрос 3. Для чего используется критерий знаков?
1. Для приближенного определения медианы случайной величины Х
2. Для приближенного определения дисперсии
3. Для проверки гипотезы о том, что некоторое число является медианой распределения случайной величины Х
4. Для проверки гипотезы о том, что случайная величина Х имеет биноминальное распределение
5. Для проверки гипотезы о значении случайной величины s(x) = 1 при х > 0 и s(x) = 0 при х < 0
Вопрос 4. В каком случае говорят, что распределение G0(x) принадлежит сдвиговому семейству распределений G, задаваемому распределением G(x)?
1. Если существует такая Θ , что для любого х найдется F(x) = G(x-Θ )
2. Если существует постоянная величина t0 такая, что для любого х выполняется G(x) = G0(x-t0)
3. Если медиана Θ случайной величины Х такая, что для любого х выполняется F(x) G0(x- Θ). (F(x) - распределение случайной величины Х, G0(x) - распределение случайной величины Y)
4. Если выполняется критерий знаков при медиане Θ
5. Если у случайной величины Х, задаваемой распределением G0(x), дисперсия численно равна дисперсии случайной величины Y, задаваемой распределением G(x).
Вопрос 5. Что такое статистика Манна-Уитни?
1 .Ветвь математической статистики
2. Случайная величина, равная числу выполняющихся неравенств вида х < y при i {1, …, m}, j {1, …, n}, где х1, … хm, у1, … уn две односторонние выборки
3. Результат проверки гипотезы H : F = G о совпадении законов распределений непрерывных случайных величин X, Y
4. Таблица, используемая для приближенного определения наименьшего уровня значимости
5. Любая функция, принадлежащая сдвиговому семейству, образованная гиперболическим распределением
Эта задача уже решена! Вы можете получить её за 150 руб.
Задание 14
Вопрос 1. Рассмотрим выборку 9, 7, 7, 7, 1, 2, 8, 3. В какой строке записан ранг числа 7 в этой выборке?
1. 3
2. 4
3. 4 1/2
4. 5
5. 6
Вопрос 2. Рассмотрим две независимые выборки x1, … xm; y1, … yn и ранги совокупностей наблюдений S1, … Sm+n. Что такое статистика Уилкоксона?
1. S1 + … + Sm+n
2. х1+х2+ … + хm
3. у1+у2 + … + уn
4. у1+ … + уn + х1+ … + хm
5. Сумма рангов одной из выборок
Вопрос 3. Рассмотрим две независимые выборки по 6 элементов в каждой. Каково математическое ожидание статистики Уилкоксона при выполнение гипотезы об однородности выборок?
1. 39
2. 38
3. 37
4. 35
5. 43
Вопрос 4. Какое из утверждений справедливо при отсутствии эффекта обработки для повторных парных наблюдений (x1,y1)…(xn,yn) случайных величин Х и У независимо от их распределения?
1. Р(xt > yt) > 0.5 для всех i = 1, …, n
2. Р(xt < yt) > 0.5 для всех i = 1, …, n
3. Р(xt > yt) = 0.5 для всех i = 1, …, n
4. Р(xt = yt) > 0.5 для всех i = 1, …, n
5. Р(xt = yt) > 0.5
Вопрос 5. Какое условие необходимо для применения критерия знаковых ранговых сумм Уилкоксона?
1. Р(xt > yt) = 0.5 для всех i = 1, …, n
2. Случайные величины zt = yt - xt, где i = 1, …, n, непрерывны и одинаково распределены
3. Случайные величины zt = yt - xt, где i = 1, …, n, дискретны
4. Случайные величины zt = yt - xt, где i = 1, …, n, имеют разные распределения
5.Выполнение гипотезы о нулевом эффекте обработки
Эта задача уже решена! Вы можете получить её за 150 руб.
Цена консультации по работе Контрольная по теории вероятности N0002 - договорная.
Чтобы оформить заявку на получение файла с готовой работой или заказ на консультацию и помощь с работой по указанной теме по Вашим требованиям нажмите кнопку:
